Прямоугольная система координат

Прямоугольным векторным базисом в пространстве называется тройка единичных взаимно-перпендикулярных векторов, взятых в определенном порядке.

X, i

Y, j

Z, k

M

Прямоугольная система координат в пространстве – это совокупность некоторой точки – начало координат и прямоугольного векторного базиса.

 

OM – радиус вектор.

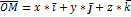
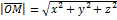
Координатная форма вектора.

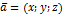
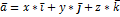
1)

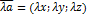
2)

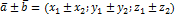
Расстояние между двумя точками

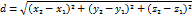
Деление отрезка в данном отношении.

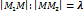
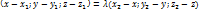
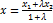
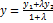
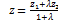
Скалярное произведение векторов.

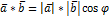
Свойства:

1) 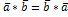- переместительный закон

2) 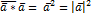– скалярный квадрат

3) 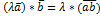- сочетательный закон

4) 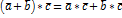- распределительный закон

5)

Уравнение прямой проходящей через две точки

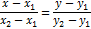
Векторное произведение векторов и его свойства

Три компланарных вектора образуют правую тройку, если с конца С кротчайший поворот от первого А ко второму В виден совершающийся против часовой стрелки, в противном случае тройка называется левой.

Векторным произведением двух векторов А В называется вектор С, обладающий следующими свойствами:

1) С┘А, С┘В

2) │С│=│А│*│В│*sinL L=(A^B)

S=│C│

3) А,В,С образуют правую тройку

 

Свойства векторного произведения

1) АхВ= -(ВхА) антиперестоновачный закон

2) АхА=0

3) (LA)хB=L(АхВ) сочетательные свойства

4) (А+В)хС=АхС+ВхС Необходимое и достаточное условие коллинеарности векторов