Уравнение прямой в пространстве проходящей через две данные точки

Общее уравнение прямой в пространстве. Приведение общих уравнение прямой к каноническому виду

-Общее уравнение прямой в пространстве

Для перехода от общих уравнений к каноническомунужно

1) Найти точку, принадлежащую прямой

2) Найти направляющий вектор прямой

Условия параллельности и перпендикулярности прямых в пространстве.Угол между прямой и плоскостью.

Две прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, а => их координаты пропорциональны.

Две прямые перпендикулярны тогда и только тогда, когда их направляющие вектора => скалярное произведение равно 0.

Дано:

=

Найти:

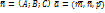
cos(

Условия параллельности и перпендикулярности прямой и плоскости.

L//q < = > Прямая и плоскость параллельны тогда и только тогда, когда нормальный вектор плоскости перпендикулярен направляющему вектору прямой, а => скалярное произведение этих векторов равно 0. Пусть L Q=> < = > Прямая плоскости тогда, и только тогда, когда нормальный вектор плоскости коллинеарен направляющему вектору прямой, а следовательно их координаты пропорциональны.