Точки разрыва и их классификация. Если хотя бы одно из условий определения 1 не выполнено, то точка является точкой разрыва

Если хотя бы одно из условий определения 1 не выполнено, то точка 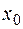является точкой разрыва. Различают следующие виды точек разрыва:

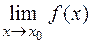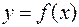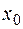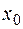1) если существует, но функция в точке не определена или определена, но то точка называется точкой устранимого разрыва;

2) если существуют конечные односторонние пределы в точке 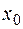, но они не равны друг другу, то точка 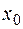называется точкой разрыва первого рода, а модуль разности 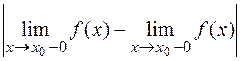— скачком функции в точке ;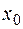

3) если хотя бы один из односторонних пределов равен ¥ или вообще не существует, то точка 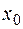называется точкой раз­рыва второго рода.

Таким образом, при исследовании функции на непрерывность необходимо проверить выполнение условий определения 1. Если 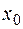— точка разрыва, то для установления характера разрыва не­обходимо вычислить односторонние пределы.