Производная и дифференциал функции: определение, геометрический смысл, уравнение касательной. Связь между дифференцируемостью и непрерывностью

Определение: Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение, стремящемся к нулю.

- уравнение касательной

y=f(x0)+f'(x0)×(x-x0)

Где f'(x0) угловой коэффициент касательной

Если функция дифференцируема в точке, то она непрерывна в этой точке.... Если х0 – точка разрыва функции, то в ней функция не дифференцируема. Утверждение, обратное теореме, не верно.

Геометрический смысл производной состоит в том, что значение производной f'(x0) равно угловому коэффициенту касательной к графику функции y=f(x) в точке с абсциссой х0.

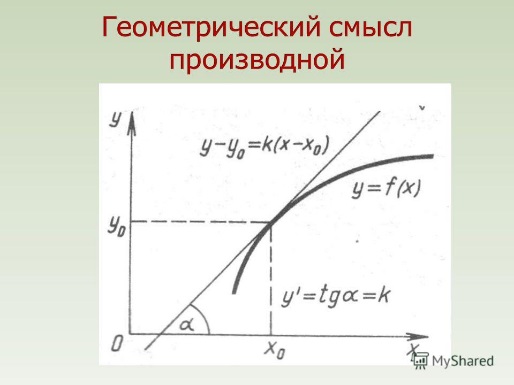
Таблица производных основных элементарных функций.

Применение дифференциала в приближенных вычислениях.

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy, (3)

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.