Производная суммы, произведения и частного.
Рассмотрим некоторые теоремы.
Теорема 1. Производная постоянной равна нулю, то есть
 , где C-const.
, где C-const.
Теорема 2. Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций
 . (5)
. (5)
Теорема 3. Производная произведения дифференцируемых функций равна
 . (6)
. (6)
Следствие. Постоянный множитель можно выносить за знак производной
 .
.
Замечание. Аналогично можно доказать формулу для произведения трех функций
 .
.
Теорема 4. Производная частного двух дифференцируемых функций равна
 . (7)
. (7)
Замечание. Для функции вида  , где C-const, рациональнее применять формулу производной произведения, а не частного:
, где C-const, рациональнее применять формулу производной произведения, а не частного:
 .
.
Производная сложной функции. Производная обратной функции
Теорема о производной сложной функции
Пусть дана сложная функция  или
или  , где
, где  так называемый промежуточный аргумент. Справедливо правило дифференцирования сложной функции.
так называемый промежуточный аргумент. Справедливо правило дифференцирования сложной функции.
Теорема. Если функция  в некоторой точке х имеет производную
в некоторой точке х имеет производную  , а функция
, а функция  при соответствующем значении u имеет производную
при соответствующем значении u имеет производную 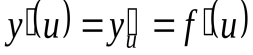 , то сложная функция
, то сложная функция  в указанной точке х также имеет производную
в указанной точке х также имеет производную 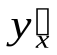 , которая равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по х:
, которая равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по х:
|
|
|
 . (8)
. (8)
Сводная таблица основных формул дифференцирования
1.  . 2.
. 2.  ,
,  ,
,  ,
,  .
.
3.  ,
,  . 4.
. 4.  ,
,  .
.
5.  . 6.
. 6.  7.
7.  .
.
8. 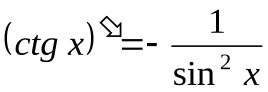 . 9.
. 9.  . 10.
. 10.  .
.
11. 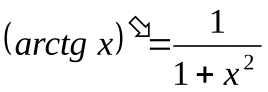 . 12.
. 12. 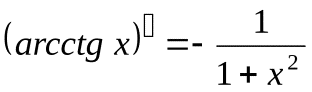 .
.
Логарифмическое дифференцирование
Определение. Операция, состоящая в последовательном применении к функции сначала логарифмирования (по основанию e), а затем дифференцирования, называется логарифмическим дифференцированием, а её результат – логарифмической производной.
 П ример. Найти производную от функции
П ример. Найти производную от функции 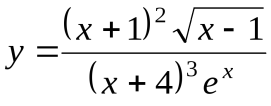 .
.
 Решение. Логарифмируя, находим
Решение. Логарифмируя, находим
 .
.
 Дифференцируем обе части полученного равенства
Дифференцируем обе части полученного равенства

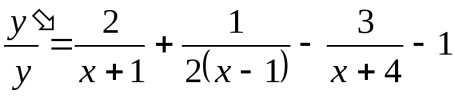 .
.

 Умножая на у и подставляя вместо у его выражение, получим
Умножая на у и подставляя вместо у его выражение, получим


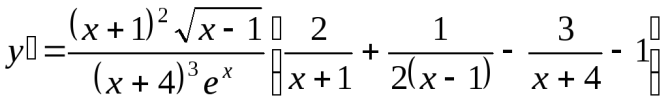 .
.
Производные обратных функций
Определение. Если каждому значению у из области изменения функции  соответствует единственное значение х, то можно говорить, что х есть функция от у
соответствует единственное значение х, то можно говорить, что х есть функция от у
 ,
,
которая называется обратной функцией по отношению к данной.
Замечание. Функции  и
и  называются ещё взаимно-обратными.
называются ещё взаимно-обратными.
Пример. Для функции  обратной функцией является
обратной функцией является  .
.
Теорема. Если функция  дифференцируема, имеет обратную функцию и
дифференцируема, имеет обратную функцию и  , то производная обратной функции существует и равна обратной величине производной данной функции, то есть
, то производная обратной функции существует и равна обратной величине производной данной функции, то есть
 или
или 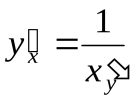 .
.
 2018-01-08
2018-01-08 1755
1755
