Бесконечно большие величины и их свойства. Связь с бесконечно малыми величинами

Функция y=f(x) называется бесконечно большой (или бесконечно большой величиной) при , если . Например, б.б.ф. при , т.к. f(x) → ∞ или y=tgx при х б.б.ф.

Аналогично определяется б.б.ф. при х→±∞, + и -.

Если f(x) → ∞ при и принимает лишь положительные значения, то пишут , если лишь отрицательные, то .

Свойства бесконечно больших функций:

1. Произведение б.б.ф. на функцию, предел которой отличен от 0, есть б.б.ф.

2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.

3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.

Связь между бесконечно малыми и бесконечно большими функциями

Теорема: Если функция α (х) – бесконечно малая при , то

функция является бесконечно большой при

, и наоборот.

 

Односторонние пределы функции.

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Левый и правый пределы функции

Число называется правым пределом функции в точке , если для такое, что для любого и 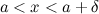, выполняется неравенство (рис. 1). Правый предел обозначается

Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 2). Левый предел обозначается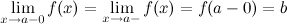

Левый и правый пределы функции называются односторонними пределами.

Теорема

Если существуют и , причем , то существует и . Обратное утверждение также верно.

В случае, если , то предел не существует.