Пусть в интервале (a, b) задана функция f (x) и в каждой точке x (a, b) существует производная f '(x). Таким образом в интервале (a, b) задана функция y = f '(x).
Если первая производная функция y = f '(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f (x).
Вторая производная обозначается символами f ''(x) или
| d 2 f |
| dx 2 |
.
Вообще, производной n–го порядка функции f (x), называется производная от производной функции f (x) (n − 1)–го порядка. Производная n –го порядка обозначается f (n) (x).
Замечание. Если речь идет о производной n –го порядка (n = 2, 3, …) в фиксированной точке x 0, то для существования f (n) (x 0) необходимо существование f (n − 1) (x) не только в точке x 0, но и в некоторой ее окрестности. При этом условии
f (n) (x 0) =
f (n − 1) (x 0). |
Функция, имеющая в точке производную n –го порядка, называется n раз дифференцируемой в этой точке.
Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.
Формулы для производных n –го порядка суммы и произведения функций
Если функции u (x) и v (x) n раз дифференцируемы на некотором промежутке, то производная n –го порядка суммы определяется формулой
| (u + v)(n) = u (n) + v (n), |
а производная n –го порядка произведения определяется формулой Лейбница
(u · v)(n) = u (n) · v + n u (n − 1) · v ' +
u (n − 2) · v '' + … + u · v (n). |
Формула Лейбница может быть записана в виде
(u · v)(n) =
Cnk · u (n − k) v (k), |
где u (0) = u (x), v (0) = v (x) и Cnk =
| n! |
| k! (n − k)! |
— биномиальные коэффициенты.
Дифференциалы высших порядков
Пусть в интервале (a, b) задана дважды дифференцируемая функция y = f (x), где x — независимая переменная.
Фиксируем приращение dx = Δ x независимой переменной x, т.е. будем считать первый дифференциал
| dy = f '(x) dx | (1) |
функцией только переменной x.
Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f (x) в точке x и обозначается d 2 f (x).
Дифференцируем выражение в правой части (1) как произведение
| d 2 f (x) = d (df (x)) = d (f '(x) dx) = f ''(x) dx · dx + f '(x) · d (dx). |
Учитывая, что d (dx) = 0, получаем формулу для вычисления второго дифференциала
| d 2 f (x) = f ''(x) dx 2. | (2) |
Пусть в интервале (a, b) функция f (x) имеет производные до n –го порядка включительно.
Дифференциалом n –го порядка называется дифференциал от дифференциала (n − 1)–го порядка
| dn f (x) = d (d (n − 1) f (x)). |
Формула для вычисления дифференциала n–го порядка
| dn f (x) = f (n) (x) dxn. |
Неинвариантность формы дифференциала порядка выше первого
Рассмотрим случай, когда х является не независимой переменной, а функцией от другой переменной
| y = f (x), x = (u). |
В силу инвариантности формы первого дифференциала имеем
| dy = f '(x) dx. | (3) |
Теперь в правой части формулы (3) от переменной u зависит не только функция f (x), но и дифференциал dx. Следовательно
| dx = '(u) du, d 2 x = ''(u) du 2. |
Таким образом, в общем случае
| d 2 y = f ''(x) dx 2 + f '(x) d 2 x. | (4) |
Сравнивая формулы (2) и (4), убеждаемся, что дифференциалы второго (и более высоких порядков) не обладают инвариантностью формы.
Правило Лопиталя
Если 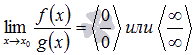 , и если функции f(x) и g(x) –
, и если функции f(x) и g(x) –
дифференцируемы в окрестности точки 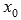 , то
, то 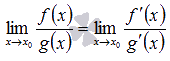
В случае, когда неопределенность не исчезает после применения правила Лопиталя, то его можно применять вновь.
Рассмотрим несколько примеров и подробно разберем решения.
Пример.
Вычислить предел, используя правило Лопиталя 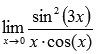
Решение.
Подставляем значение
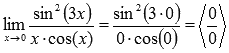
Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:
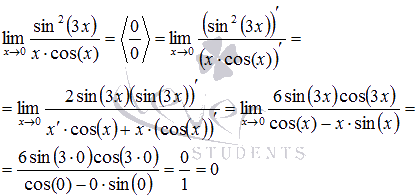
Ответ:
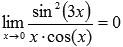
 2018-01-08
2018-01-08 1079
1079
