Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
Для определения выпуклости (вогнутости) функции на некотором интервале можно использовать следующие теоремы.
Теорема 1. Пусть функция 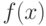 определена и непрерывна на интервале
определена и непрерывна на интервале 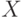 и имеет конечную производную
и имеет конечную производную 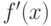 . Для того, чтобы функция
. Для того, чтобы функция 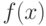 была выпуклой (вогнутой) в
была выпуклой (вогнутой) в 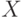 , необходимо и достаточно, чтобы ее производная
, необходимо и достаточно, чтобы ее производная 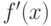 убывала (возрастала) на этом интервале.
убывала (возрастала) на этом интервале.
Теорема 2. Пусть функция 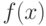 определена и непрерывна вместе со своей производной
определена и непрерывна вместе со своей производной 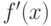 на
на 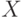 и имеет внутри
и имеет внутри 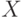 непрерывную вторую производную
непрерывную вторую производную 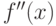 . Для выпуклости (вогнутости) функции
. Для выпуклости (вогнутости) функции 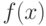 в
в 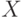 необходимо и достаточно, чтобы внутри
необходимо и достаточно, чтобы внутри 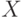
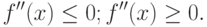
 2018-01-08
2018-01-08 1551
1551








