Точки перегиба. Необходимое и достаточное условие перегиба

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.

Из этого определения следует, что точки перегиба — это точки точки экстремума первой производной. Отсюда вытекают следующие утверждения для необходимого и достаточного условий перегиба.

Теорема (необходимое условие перегиба). Для того чтобы точка являлась точкой перегиба дважды дифференцируемой функции 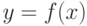, необходимо, чтобы ее вторая производная в этой точке равнялась нулю (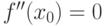) или не существовала.

Теорема (достаточное условие перегиба). Если вторая производная 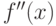дважды дифференцируемой функции 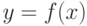при переходе через некоторую точку меняет знак, то есть точка перегиба.

Отметим, что в самой точке вторая производная 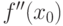может не существовать.