Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки ( ) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.
) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.
Асимптоты бывают 3 видов: вертикальные (а), горизонтальные (б) и наклонные (в). 
Асимптоты находят, используя следующие теоремы:
Теорема 1. Пусть функция 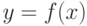 определена в некоторой окрестности точки
определена в некоторой окрестности точки  (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при
(исключая, возможно, саму эту точку) и хотя бы один из пределов функции при  (слева) или
(слева) или  (справа) равен бесконечности. Тогда прямая является
(справа) равен бесконечности. Тогда прямая является  вертикальной асимптотой графика функции
вертикальной асимптотой графика функции 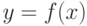 .
.
Вертикальные асимптоты  следует искать в точках разрыва функции
следует искать в точках разрыва функции 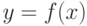 .
.
Теорема 2. Пусть функция 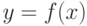 определена при достаточно больших
определена при достаточно больших  и существует конечный предел функции
и существует конечный предел функции
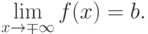
Тогда прямая  есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 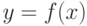 .
.
Теорема 3. Пусть функция 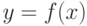 определена при достаточно больших
определена при достаточно больших  и существуют конечные пределы
и существуют конечные пределы


Тогда прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 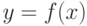 .
.
 2018-01-08
2018-01-08 1339
1339
