Условие монотонности дифференцируемой функции

Функция у = f (х) называется возрастающей (убывающей) на некотором промежутке, если для любых значений x₂>x₁ этого промежутка выполняется условие f (x₂) > f (x₁)(f (x₂) < f (x₁)).

Функция у = f (х) имеет максимум (минимум) в точке x₀, если существует такая окрестность точки x₀, что для всех x, принадлежащих этой окрестности, выпол­няется условие f (х) < f (х₀)(f (х) > f (х₀), х¹ х₀.

Интервал, на котором функция возрастает или убывает, называется интервалом монотонности функции.

Теорема 1. (необходимое условие монотонности функции). Если дифференцируе­мая в интервале (а, b) функция у = f (х) возрастает (убывает) на этом интервале, то ее производная в каждой точке (а, b) .

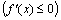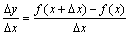Доказательство. Пусть у = f (х) – дифференцируема и возрастает на (а_, b). Пусть точки х и х+ х принадлежат (а_, b). Если >0, то f (x+ ) > f (x); если <0, то f (x + ) < f (x). В обоих случаях > 0. Переходя к пределу в последнем неравенстве при 0 и учитывая, что функция дифференцируема, получаем .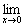

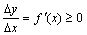Аналогично доказывается теорема в случае убывающей функции. Рекомендуем сделать это самостоятельно.

Теорема 2. (достаточное условие монотонности функции). Если непрерывная на отрезке [ а, b ] функция у = f (х) в каждой точке интервала (а, b) имеет положи­тельную (отрицательную) производную, то эта функция возрастает (убывает) на отрезке [ а, b ].

Доказательство. Пусть 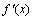>0 для всех хÎ (а,b). Рассмотрим два произвольных значения x₂ > x₁, принадлежащих [ а, b ]. По формуле Лагранжа 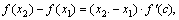х₁<с < х₂. 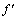(с) > 0 и х₂ – х₁ > 0, поэтому 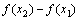> 0, откуда > 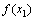, то есть функция f(х) возрастает на отрезке [ а, b ]. Аналогично доказывается вторая часть теоремы.