Задача 1. Найти указанные пределы:
1.1. а) 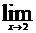
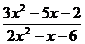 ; б)
; б) 

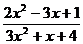 ;
;
в) 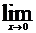
 ; г)
; г) 

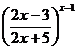 .
.
1.2. а) 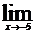
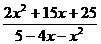 ; б)
; б) 

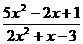 ;
;
в) 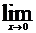
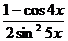 ; г)
; г) 
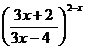 .
.
1.3. а) 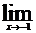
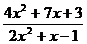 ; б)
; б) 
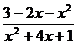 ;
;
в) 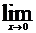
 ; г)
; г) 
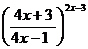 .
.
1.4. а) 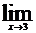
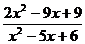 ; б)
; б) 
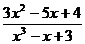 ;
;
в) 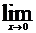
 ; г)
; г) 
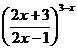 .
.
1.5. а) 
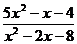 ; б)
; б) 
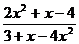 ;
;
в) 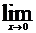
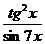 ; г)
; г) 
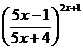 .
.
1.6. а) 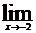
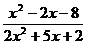 ; б)
; б) 
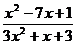 ;
;
в) 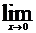
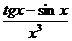 ; г)
; г) 
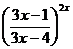 .
.
1.7. а) 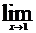
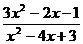 ; б)
; б) 
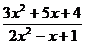 ;
;
в) 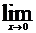
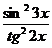 ; г)
; г) 
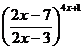 .
.
1.8. а) 
 ; б)
; б) 
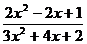 ;
;
в) 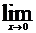
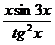 ; г)
; г) 
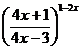 .
.
1.9. а) 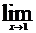
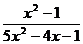 ; б)
; б) 
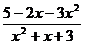 ;
;
в) 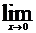
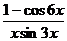 ; г)
; г) 
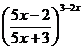 .
.
1.10. а) 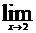
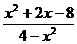 ; б)
; б) 
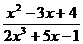 ;
;
в) 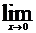 sin2xctg5x; г)
sin2xctg5x; г) 
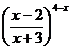 .
.
Задача 2. Найти производные следующих функций, пользуясь правилами и формулами дифференцирования:
2.1. а) y= (3x-4 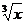 +2)4; б) y=
+2)4; б) y= 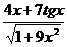 ;
;
в) y= cos3xesinx; г) ln arctg2x.
2.2. a) y= (3x3-2 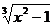 )2; б) y=
)2; б) y= 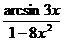 ;
;
в) y= 23x· tg2x; г) y= cosln5x.
2.3. а) y= (x2- 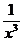 +5
+5 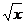 )4; б) y=
)4; б) y= 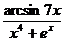 ;
;
в)y= etgx · ln2x; г) y= cos  .
.
2.4. а) y= (4x2- 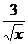 +4)3; б)y=
+4)3; б)y= 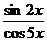 ;
;
в) y=28x· tg 3x; г)y= arcsinln 4x.
2.5. а) y= (x5- 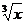 +1)5; б) y=
+1)5; б) y= 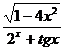 ;
;
в) y= ectgx · sin 4x; г) y= sinln5x.
2.6. а) y= (6x2- 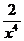 +5)2; б) y=
+5)2; б) y=  ;
;
в) y= 3tgx· arcsin(x2); г) y= ln sin6x.
2.7. а) y= (x3 - 4 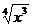 + 2)3; б) y=
+ 2)3; б) y= 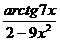 ;
;
в) y= ectg x · cos 6 x; г) y= sin ln2x.
2.8. а) y= (x2 - 2 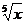 + 4)4; б) y=
+ 4)4; б) y=  ;
;
в) y= 4 cos x · arctg 2 x; г) y= ln sin5x.
2.9. a) y= (3x5- 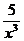 - 2)5; б) y=
- 2)5; б) y= 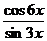 ;
;
в) 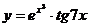 ; г)
; г) 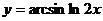 .
.
2.10. a) y= (x4 - 2 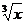 + 1)2; б) y=
+ 1)2; б) y= 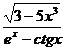 ;
;
в) y= 2 sin x · arcsin 2x; г) y= ln cos7x.
Задача 3. Исследовать заданные функции методом дифференциального исчисления и начертить их графики по следующей схеме: 1) найти область определения функции; 2) найти точки экстремума функции и определить интервалы её монотонности; 3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика; 4) найти асимптоты графика функции; 5) построить график.
3.1. y = 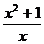 . 3.2. y =
. 3.2. y = 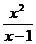 .
.
3.3. y = 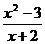 . 3.4. y =
. 3.4. y = 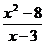 .
.
3.5. y =  . 3.6. y =
. 3.6. y = 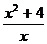 .
.
3.7. y= 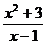 . 3.8. y =
. 3.8. y = 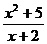 .
.
3.9. y = 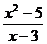 . 3.10. y =
. 3.10. y = 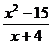 .
.
Задача 4. Найти неопределённые интегралы:
4.1. а) 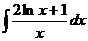 ; б)
; б)  ;
;
в) 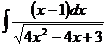 ; г)
; г) 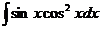 .
.
4.2. а)  ; б)
; б) 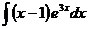 ;
;
в) 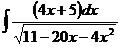 ; г)
; г)  .
.
4.3. а) 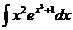 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4.4. а)  ; б)
; б) 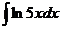 ;
;
в) 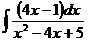 ; г)
; г)  .
.
4.5. а) 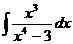 ; б)
; б) 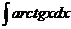 ;
;
в) 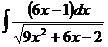 ; г)
; г) 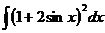 .
.
4.6. а) 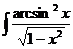 ; б)
; б) 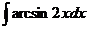 ;
;
в) 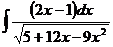 ; г)
; г)  .
.
4.7. а) 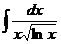 ; б)
; б) 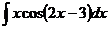 ;
;
в) 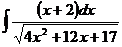 ; г)
; г)  .
.
4.8. а) 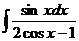 ; б)
; б) 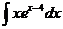 ;
;
в) 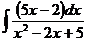 ; г)
; г) 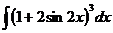 .
.
4.9. а) 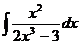 ; б)
; б)  ;
;
в) 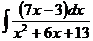 ; г)
; г) 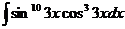
4.10. а) 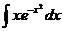 ; б)
; б) 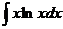 ;
;
в) 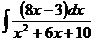 ; г)
; г) 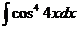 .
.
Задача 5. В задачах 5.1-5.6 вычислить площадь фигуры, ограниченной заданными линиями:
5.1. y= x2, y= 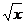 . 5.4. y = 2x2, x + y = 3, y = 0.
. 5.4. y = 2x2, x + y = 3, y = 0.
5.2. y= x, xy= 1, x= 4. 5.5. 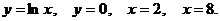
5.3. y= 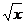 , x+ y= 2, y= 0. 5.6.
, x+ y= 2, y= 0. 5.6. 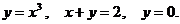
В задачах 5.7-5.10 вычислить объем тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями:
5.7.y= x2, y= 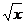 . 5.9. y= x, xy= 1, x= 2, y= 0.
. 5.9. y= x, xy= 1, x= 2, y= 0.
5.8. y= 3x2, y= 3x. 5.10. y = 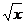 , x + y = 2, x = 0.
, x + y = 2, x = 0.
Задача 6. Найти частные решения линейных дифференциальных уравнений первого порядка:
6.1. 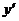 + 2y tg2x= sin4x; y (0)= 0. 6.6.
+ 2y tg2x= sin4x; y (0)= 0. 6.6. 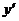 + y tgx= sin2x; y(0)= 1.
+ y tgx= sin2x; y(0)= 1.
6.2. 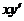 - y= x2 cos x;
- y= x2 cos x; 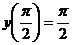 . 6.7.
. 6.7. 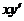 - y= x lnx; y(1)= -1.
- y= x lnx; y(1)= -1.
6.3. 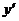 sin x – y cosx = 1; y
sin x – y cosx = 1; y 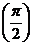 = 0. 6.8.
= 0. 6.8. 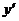 - 2xy= 2x
- 2xy= 2x 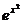 ; y (0)= e.
; y (0)= e.
6.4. 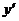 +2xy= 3x2
+2xy= 3x2  ; y(0)= 0. 6.9
; y(0)= 0. 6.9 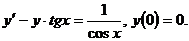
6.5. 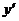 cosx+ y sinx= 1; y(0)= 0. 6.10.
cosx+ y sinx= 1; y(0)= 0. 6.10. 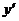 +2xy= x
+2xy= x  ; y(0)= 1.
; y(0)= 1.
Задача 7. Из всех товаров, продаваемых магазином, N1 процентов выпущено на предприятиях первойфирмы, N2процентов - второй, N3 - третьей. Первойфирмой производится n1 – процентов товаров высшего качества, второй – n2 процентов, а третьей– n3 процентов. Найти вероятность покупки товара высшего качества.
7.1. N1=30; N2=40; N3=30; n1=60; n2=70; n3=70.
7.2. N1=50; N2=30; N3=20; n1=60; n2=60; n3=70.
7.3. N1=50; N2=20; N3=30; n1=50; n2=60; n3=50.
7.4. N1=40; N2=40; N3=20; n1=70; n2=70; n3=40.
7.5. N1=40; N2=30; N3=30; n1=80; n2=70; n3=60.
7.6. N1=30; N2=50; N3=20; n1=80; n2=80; n3=50.
7.7. N1=60; N2=20; N3=20; n1=70; n2=80; n3=60.
7.8. N1=20; N2=40; N3=40; n1=60; n2=80; n3=80.
7.9. N1=20; N2=50; N3=30; n1=60; n2=90; n3=70.
7.10. N1=20; N2=30; N3=50; n1=40; n2=50; n3=80.
Задача8. Испытывается устройство, состоящееnнезависимо работающих приборов. Вероятность отказа каждого прибора равна p. Составить закон распределения числа отказавшихприборов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
8.1. n=5; p=0,2. 8.6. n=4; p=0,2.
8.2.n=5; p=0,4. 8.7. n=4; p=0,4.
8.3. n=5; p=0,5. 8.8. n=4; p=0,5.
8.4. n=5; p=0,6. 8.9. n=4; p=0,6.
8.5. n=5; p=0,8. 8.10. n=4; p=0,8.
 2018-01-08
2018-01-08 1289
1289
