2018-01-08
1132
Пусть известно статистическое распределение признака X, 
- число наблюдений, при которых наблюдалось значение признака, меньшее x, n - общее число наблюдений (объем выборки). Ясно, что относительная частота события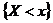 
равна 
. Если x изменяется, то изменяется и относительная частота, т.е. есть функция от x. Так. Как она находится эмпирическим путем, то называется эмпирической.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию 
, определяющую для любого x относительную частоту события 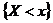. Итак, по определению:
,
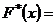
где - число вариант, меньших x, n – объем выборки.
Функцию распределения 
генеральной совокупности называют теоретической функцией распределения.
По теореме Бернулли:
-
теорема Гливенко.
Таким образом, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения выборки.
Пример 3.
Построить эмпирическую функцию по данному распределению выборки:
 | |||
 |
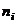Объем выборки n =12+18+30=60.
1) x 
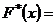0;
2) 
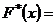12/60=0,2;
3) 
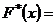30/60=0,5;
4) 
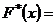1.
