Числовые характеристики выборочного метода

Пусть 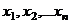– выборка объема n из генеральной совокупности с функцией распределения . Рассмотрим выборочное распределение, принимающее значения 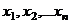с вероятностями, равными . Т.к. выборка случайна, то и ее числовые характеристики эмпирического распределения случайные величины, которые называются эмпирическими числовыми характеристиками.

Эмпирическим (или выборочным) математическим ожиданием называется среднее арифметическое элементов выборки:

.

Выборочная дисперсия равна:

.

Можно воспользоваться формулой:

,

где .

Выборочной модой унимодального (одновершинного) распределения называют элемент выборки, встречающийся с наибольшей частотой.

Выборочной медианой называется число , делящее вариационный ряд на две части, содержащие равное число элементов. Если n – нечетное число, то – элемент выборки со средним номером, если , то .