По теме: Дифференциальные уравнения первого порядка
для всех направлений бакалавриата
Уфа 2012
УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)
Составители: доцент Лукманов Р.Л.
доцент Маннанов М.М.
Рецензент: доцент кафедры физики Шайхитдинов Р.З.
Ответственный за выпуск: зав. кафедрой математики
доцент Лукманов Р.Л.
Введение
При работе с данным методическим пособием студентам рекомендуется изучить соответствующий теоретический материал по учебникам [1] – [3]. Большое количество решенных примеров представлено в руководстве к решению задач [7].
Приведем основные понятия и определения.
Обыкновенным дифференциальным уравнением n-порядка называется уравнение вида
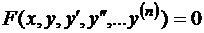 , (1)
, (1)
где 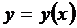 неизвестная функция, а
неизвестная функция, а 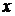 - ее аргумент.
- ее аргумент.
Решением уравнения (1) называется любая функция, которая обращает равенство (1) в тождество. В тех случаях, когда уравнение (1) удается записать в виде
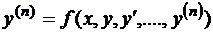 , (2)
, (2)
говорят, что уравнение (1) разрешено относительно старшей производной. Например, уравнение первого порядка, разрешенное относительно старшей производной, имеет вид:
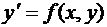 . (3)
. (3)
Заметим, что если правая часть уравнения (3) не зависит от  , то есть
, то есть
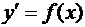 (4)
(4)
то решение дифференциального уравнения (4) эквивалентно нахождению неопределенного интеграла от функции 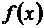 , поскольку, проинтегрировав обе части уравнения (4), получим:
, поскольку, проинтегрировав обе части уравнения (4), получим:
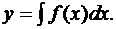
Например, все решения уравнения
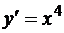
задаются равенством
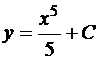 .
.
Как видим, это дифференциальное уравнение имеет бесконечно много решений. Эта ситуация типична для всех дифференциальных уравнений. Поскольку дифференциальные уравнения возникают при моделировании реальных явлений и процессов, то для однозначного определения решения должны быть заданы (одно или несколько, в зависимости от порядка уравнения) дополнительные условия. Эти условия возникают естественным образом, исходя из дополнительной информации о решении. Например, для дифференциального уравнения первого порядка таким дополнительным условием является равенство:
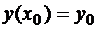 , (5)
, (5)
где 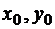 - заданные числа. Например, если
- заданные числа. Например, если  играет роль времени, а
играет роль времени, а 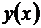 - скорость, то условие (5) означает, что известна скорость в начальный момент времени
- скорость, то условие (5) означает, что известна скорость в начальный момент времени 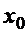 . Поэтому условие (5) обычно называют начальным.
. Поэтому условие (5) обычно называют начальным.
Известна теорема, гарантирующая, что при определенных условиях на функцию 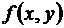 задача нахождения функции
задача нахождения функции 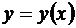 , удовлетворяющей дифференциальному уравнению (3) и начальному условию (5), имеет решение, причем единственное.
, удовлетворяющей дифференциальному уравнению (3) и начальному условию (5), имеет решение, причем единственное.
Задачу (3), (5) называют задачей Коши для дифференциального уравнения 1-го порядка.
Для дифференциального уравнения 2-го порядка задача Коши имеет вид: 

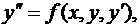 (6)
(6)
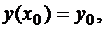
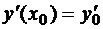 , (7)
, (7)
где 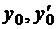 - заданные числа.
- заданные числа.
Например, если 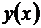 - скорость, то условия (7) означают, что в начальный момент времени
- скорость, то условия (7) означают, что в начальный момент времени 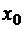 известны скорость
известны скорость 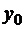 и ускорение
и ускорение 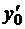 . Для дифференциального уравнения n -го порядка в качестве начальных условий задаются значения функции
. Для дифференциального уравнения n -го порядка в качестве начальных условий задаются значения функции 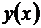 и ее производных до n-1-го порядка при
и ее производных до n-1-го порядка при
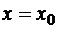 :
:
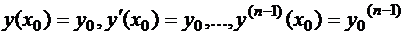 . (8)
. (8)
В данной методической разработке будут рассмотрены уравнения первого порядка и методы решения основных типов таких уравнений.
Уравнения с разделенными и разделяющимися переменными
Уравнение вида
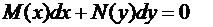 (9)
(9)
называют уравнением с разделенными переменными. Для его решения достаточно проинтегрировать обе части. Заметим, что уравнение (9) можно было записать в виде
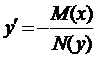 ,
,
поэтому оно является частным случаем уравнения (3).
Пример 1 Решить задачу Коши
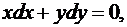 (10)
(10)
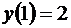 . (11)
. (11)
Решение:
Сначала найдем все решения дифференциального уравнения, а затем выберем из них то, которое удовлетворяет условию (11) (обычно так и решают задачу Коши для дифференциального уравнения). Проинтегрировав обе части дифференциального уравнения, получим:
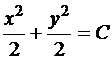 , (12)
, (12)
где 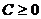 ,
,
или
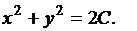 (13)
(13)
Все решения уравнения (10) задаются уравнением (13). Поскольку неизвестная функция 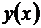 здесь задана неявным уравнением, то равенство (13) называют общим интегралом дифференциального уравнения (10). Если решение
здесь задана неявным уравнением, то равенство (13) называют общим интегралом дифференциального уравнения (10). Если решение 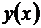 удается выписать явно, то говорят об общем решении. В нашем случае общее решение:
удается выписать явно, то говорят об общем решении. В нашем случае общее решение:
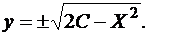 (14)
(14)
Заметим, что равенство (13) задает семейство окружностей радиуса 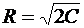 . Выберем теперь постоянную C так, чтобы решение удовлетворяло начальному условию (11). Для этого подставим в равенство (13)
. Выберем теперь постоянную C так, чтобы решение удовлетворяло начальному условию (11). Для этого подставим в равенство (13) 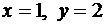 , (можно было подставить в (14)). Получим уравнение 1+4=2C. Итак, решение задачи Коши (10), (11) задается уравнением
, (можно было подставить в (14)). Получим уравнение 1+4=2C. Итак, решение задачи Коши (10), (11) задается уравнением 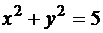 и представляет собой окружность радиуса
и представляет собой окружность радиуса 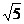 . Заметим, что задачу (10), (11) можно было сформулировать и так: среди всех кривых, уравнения которых удовлетворяют (10), найти ту, которая проходит через точку
. Заметим, что задачу (10), (11) можно было сформулировать и так: среди всех кривых, уравнения которых удовлетворяют (10), найти ту, которая проходит через точку 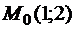 .
.
Уравнение вида
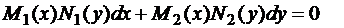 (15)
(15)
называют уравнением с разделяющимися переменными. В нем переменные можно разделить, т.е. получить уравнение вида (10), если поделить обе части на произведение 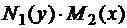 при условии, что
при условии, что 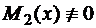 ,
, 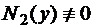 :
:
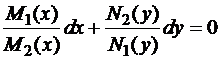 .
.
При этом те функции 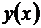 , при которых
, при которых 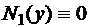 , выпадут из поля зрения и поэтому эти функции нужно подставить в исходное уравнение и проверить, не являются ли они решениями.
, выпадут из поля зрения и поэтому эти функции нужно подставить в исходное уравнение и проверить, не являются ли они решениями.
Пример 2 Найти общее решение уравнения
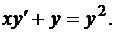 (16)
(16)
Решение:
Перепишем уравнение в виде 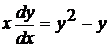 , откуда следует
, откуда следует 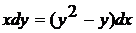 . Как видим, это уравнение с разделяющимися переменными. Поделим обе части на произведение
. Как видим, это уравнение с разделяющимися переменными. Поделим обе части на произведение 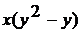 при условии, что
при условии, что 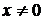 ,
, 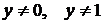 . Получим
. Получим
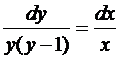 .
.
 Поскольку переменные разделились, то достаточно проинтегрировать обе части:
Поскольку переменные разделились, то достаточно проинтегрировать обе части:
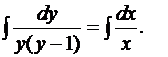 (17)
(17)
Интеграл справа табличный. Найдем интеграл от левой части. Подынтегральное выражение является правильной рациональной дробью, поэтому она представляется в виде суммы простейших дробей:

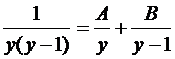 .
.
Найдем 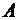 и
и 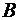 из тождества
из тождества
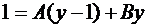 ,
,
положив в нем 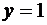 и
и  :
:
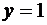
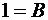 ,
,

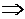
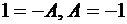 .
.
Итак,
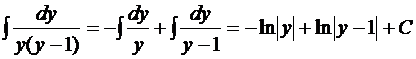 .
.
Тогда из (17) получаем
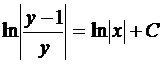 .
.
Постоянную С запишем в виде 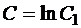 , где
, где 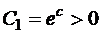 .
.
Тогда 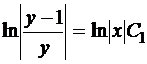 ,
,
откуда 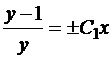 .
.
Пусть 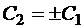 . Отметим, что
. Отметим, что 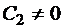 .
.
Тогда 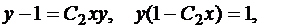
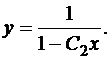 (18)
(18)
Итак, все функции, задаваемые равенством (18) при различных 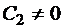 , являются решениями уравнения (16). Но мы еще должны проверить, не являются ли решениями функции
, являются решениями уравнения (16). Но мы еще должны проверить, не являются ли решениями функции 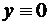 и
и 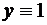 . Подставляя в уравнение (16), убеждаемся, что да. Таким образом, мы должны к решению, задаваемому равенством (18), добавить эти две функции. Поскольку при
. Подставляя в уравнение (16), убеждаемся, что да. Таким образом, мы должны к решению, задаваемому равенством (18), добавить эти две функции. Поскольку при 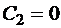 равенство (18) дает функцию
равенство (18) дает функцию 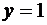 , то ответ можно записать следующим образом:
, то ответ можно записать следующим образом:
Ответ: 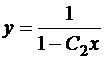 ,
, 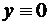 .
.
К уравнениям с разделяющимися переменными легко сводятся дифференциальные уравнения следующего вида:
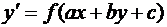 , (19)
, (19)
то есть когда аргумент правой части есть линейная функция переменных  и
и  . Введем новую неизвестную функцию
. Введем новую неизвестную функцию 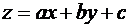 . Тогда
. Тогда
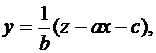
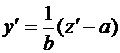
и уравнение (19) примет вид
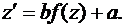
Переменные в нем легко разделяются.
Пример 3
 . (20)
. (20)
Положив 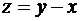 получим
получим 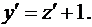
Уравнение (20) примет вид:
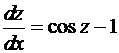 , (21)
, (21)
откуда
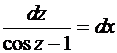 , при условии
, при условии 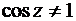 ,
,
т.е. 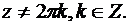
Поскольку переменные разделились, проинтегрируем обе части:
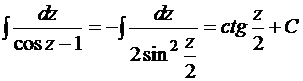 .
.
Итак:
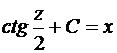
или
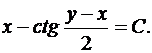
Поскольку функции 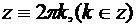 удовлетворяют уравнению (21), то к полученному общему интегралу нужно добавить функции
удовлетворяют уравнению (21), то к полученному общему интегралу нужно добавить функции
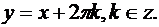
Ответ: 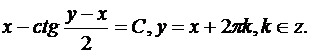
Однородные уравнения
Функция 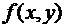 называется однородной функцией степени
называется однородной функцией степени  , если
, если
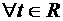
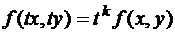 . (22)
. (22)
Например, функция 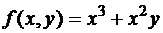 является однородной функцией степени 3. Действительно,
является однородной функцией степени 3. Действительно,
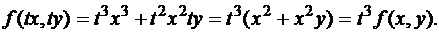
Функция 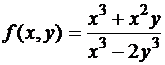 является однородной функцией нулевой степени:
является однородной функцией нулевой степени:
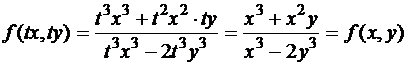 .
.
Дифференциальное уравнение  называют однородным, если правая часть
называют однородным, если правая часть 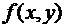 есть однородная функция нулевой степени.
есть однородная функция нулевой степени.
Поскольку условие однородности, причем нулевой степени, является очень жестким, однородные уравнения представляют очень узкий класс дифференциальных уравнений первого порядка.
Однородные функции нулевой степени хороши тем, что могут быть представлены в виде функции одного аргумента 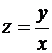 . А именно,
. А именно, 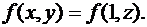 Например, функцию
Например, функцию 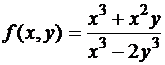 можно записать в виде
можно записать в виде 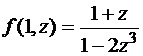 . Это следует из (22) при
. Это следует из (22) при 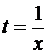 . Поэтому введение новой неизвестной функции
. Поэтому введение новой неизвестной функции 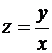 позволяет свести однородное уравнение I-го порядка к уравнению с разделяющимися переменными. Действительно, поскольку
позволяет свести однородное уравнение I-го порядка к уравнению с разделяющимися переменными. Действительно, поскольку 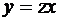 и
и 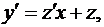 то получаем уравнение:
то получаем уравнение:
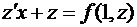 ,
,
или
 .
.
Отсюда при 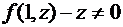 получаем уравнение с разделяющимися переменными
получаем уравнение с разделяющимися переменными 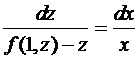 .
.
Пример 4
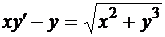 . (23)
. (23)
Запишем это уравнение в виде
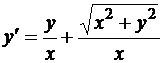 .
.
Поскольку
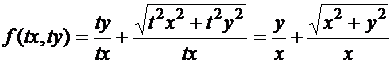 ,
,
то это уравнение однородное.
Введя в рассмотренную функцию 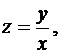 получим уравнение
получим уравнение
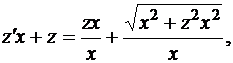
или
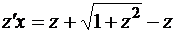
Отсюда

Разделим переменные
 .
.
Проинтегрировав обе части, получим:
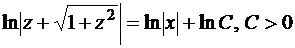 .
.
Отсюда
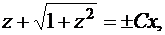
или
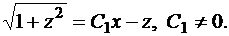
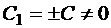
Возведем обе части в квадрат:
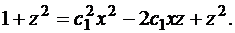
Выразим 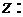
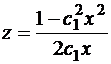 .
.
Поскольку 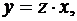 окончательно получаем:
окончательно получаем:
Ответ: 
К однородному сводятся уравнения вида
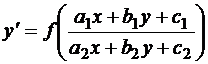 , (24)
, (24)
если 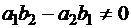 .
. 
 2018-01-08
2018-01-08 1536
1536