Уравнения в полных дифференциалах

Уравнения вида

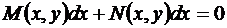(51)

называют уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции Ф, т.е.

.

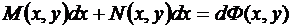Известна теорема, утверждающая, что при непрерывности функций 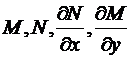условие

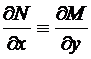
является необходимым и достаточным условием того, чтобы левая часть равенства (51) была полным дифференциалом.

Ясно, что общий интеграл дифференциального уравнения в полных дифференциалах 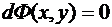представляется равенством .

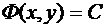При этом

(52)

где 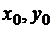- некоторые числа.

Пример 12

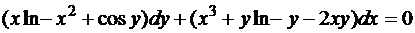. (53)

Поскольку при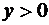

,

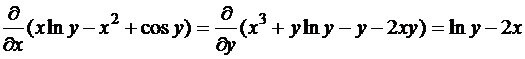то левая часть уравнения (53) является полным дифференциалом некоторой функции 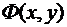, которую найдем по формуле (52)

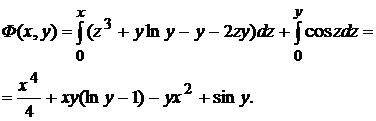
Приложение А

Задачи к РГР