

и подобрать постоянные  и
и  таким образом, чтобы
таким образом, чтобы
 . (25)
. (25)
При этом  , а правая часть есть однородная функция нулевой степени.
, а правая часть есть однородная функция нулевой степени.
Если же  , то
, то  при некотором k, т.е. коэффициенты при
при некотором k, т.е. коэффициенты при  и
и  в числителе и знаменателе пропорциональны.
в числителе и знаменателе пропорциональны.
В этом случае уравнение  заменой
заменой 
 сводится к уравнению с разделяющимися переменными.
сводится к уравнению с разделяющимися переменными.
Пример 5
 . (26)
. (26)
Запишем уравнение в виде:
 . (27)
. (27)
Это уравнение вида  с
с 

Поскольку



то применим замену
 .
.
Тогда


Последнее выражение будет однородным нулевой степени при
 (28)
(28)
Решим эту систему:

Таким образом, после замены
 (29)
(29)
уравнение (27) приводится к однородному
 (30)
(30)
Сделаем замену  Тогда
Тогда  и уравнение (30) примет вид
и уравнение (30) примет вид

откуда

 , (31)
, (31)
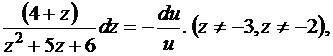

Проинтегрируем обе части. Найдем интеграл от левой части методом неопределенных коэффициентов:


При 
При 
Итак 
В итоге получим:





 .
.
Вернёмся к переменным х и у с помощью равенств (29):

 (32)
(32)
Заметим,что функции  и
и  удовлетворяют уравнению (31)
удовлетворяют уравнению (31)
и потому эти решения потеряны при разделении переменных.Запишем
эти функции в переменных  и
и  :
:


Пример 6
 (33)
(33)
Поскольку коэффициенты при х и у в числителе и знаменателе пропорциональны:

то нужно сделать замену  .
.
Тогда  и уравнение (33) примет вид:
и уравнение (33) примет вид: 

или

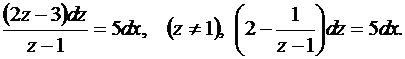
Интегрируя обе части, получим

Положив  и подставив
и подставив  получим
получим 
Ответ: 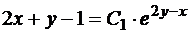 .
.
Линейные уравнения
Уравнение вида
 (34)
(34)
называется линейным уравнением первого порядка. Другими словами, линейными называют уравнения, в которые неизвестная фукнция y и её производная  входят в первой степени. Есть несколько методов решения линейных уравнений. Наиболее употребительным являются следующий.
входят в первой степени. Есть несколько методов решения линейных уравнений. Наиболее употребительным являются следующий.
Ищем решение в виде произведения двух функций:  Тогда уравнение (34) примет вид
Тогда уравнение (34) примет вид
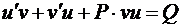 или
или 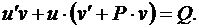 (35)
(35)
Поскольку одну из функций u или v можно выбрать достаточно произвольно, найдем функцию v из условия, что выражение в скобках равно нулю:
 . (36)
. (36)
Это уравнение с разделяющимися переменными. Допустим, мы нашли его общее решение. Возьмём одно из этих решений (ненулевое) и подставим в (35). Получим уравнение:
 (37)
(37)
c уже известной функцией v(x).
Это тоже уравнение с разделяющимися переменными. Найдя его общее решение  получим общее решение исходного уравнения (34)
получим общее решение исходного уравнения (34) 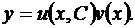
Таким образом, решение линейного уравнения (34) мы свели к последовательному решению уравнений (36) и (37) с разделяющимися переменными.
Пример 7
 (38)
(38)
Решение:
Пусть  .Тогда
.Тогда 
или
 (39)
(39)
Ищем v из уравнения
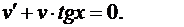 (40)
(40)
В этом уравнении переменные разделяются:

Поскольку нам достаточно получить одно из решений уравнения (40),
выберем v=cosx (взяли знак “+” и  ). Подставив эту фнкцию в (39),получим:
). Подставив эту фнкцию в (39),получим:

Итак, общее решение уравнения (38)

 2018-01-08
2018-01-08 806
806








