Есть несколько типов дифференциальных уравнений первого порядка, сводящихся к линейным. Один из них - уравнение Бернулли:
 (39)
(39)
Заметим, что n-не обязательно целое число. Будем считать, что  (иначе это уравнение будет линейным). Разделим обе части уравнения на
(иначе это уравнение будет линейным). Разделим обе части уравнения на  :
:

Если ввести в рассмотрение новую неизвестную функцию  то это уравнение примет вид:
то это уравнение примет вид:
 (40)
(40)
Это уже линейное уравнение. Но на практике выгоднее не заниматься переходом к линейному уравнению (40), а сразу решать уравнение (39) тем же методом, что и линейное, т.е. подставкой 
Пример 8
 (41)
(41)
Решение:
Разделим обе части на х:

Пусть y=uv. Тогда

 (42)
(42)
Найдём v из условия
 .
.
Тогда


Выберем одно из решений 
 Подставим его в (42):
Подставим его в (42):



 .
.

Итак,

 (44)
(44)
Заметим, что  также является решением уравнения (43),но оно включается в решение (44) при
также является решением уравнения (43),но оно включается в решение (44) при 
Итак, получаем общее решение исходного уравнения (41):
Ответ. 
К линейным также сводятся уравнения вида:
 (45)
(45)
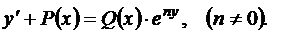 (46)
(46)
В первом из них введением новой неизвестной функции  получим линейное уравнение:
получим линейное уравнение:
 (47)
(47)
Уравнение (46) сводится к линейному уравнению 
с помощью замены 
Пример 9
 (48)
(48)
Поскольку это уравнение вида (45) с  то, применив замену
то, применив замену  получим линейное уравнение
получим линейное уравнение
 .
.
Решив его (рекомендуем сделать это самостоятельно),получим: 
откуда получаем общий интеграл исходного уравнения:

Пример 10


 Это уравнение вида (46),поэтому сделаем замену
Это уравнение вида (46),поэтому сделаем замену 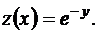 Получим линейное уравнение
Получим линейное уравнение 
 Его решение (получите его самостоятельно):
Его решение (получите его самостоятельно):
 ,
,
откуда


5 Обмен ролями между функцией и аргументом 
Возможны ситуации, когда дифференциальное уравнение нелинейно,но
становится линейным, если функцию и аргумент поменять ролями.
Пример 11
 (50)
(50)
Это уравнение нелинейное. Запишем его в виде 
т.е. будем считать y аргументом, а x функцией. Это уже линейное уравнение, поэтому его решение можно искать в виде произведения двух функций аргумента y: 
 .
.
Тогда:
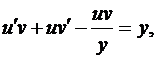
или

Из уравнения  , разделяя переменные, получим:
, разделяя переменные, получим:

Интегрируя обе части, получим v=y.
Тогда

 2018-01-08
2018-01-08 1747
1747








