В общем виде бесконечная числовая последовательность записывается следующим образом:
f(1); f(2); …;f(n); …
Если обозначить  = f(n), то получим последовательность
= f(n), то получим последовательность
 ;
;  ; ….;
; ….;  ; … или (
; … или ( ), {
), {  }.
}.
Здесь  - n – й или общий член последовательности, n - номер соответствующего члена последовательности.
- n – й или общий член последовательности, n - номер соответствующего члена последовательности.
Примеры:
5.9. Рассмотрим последовательность ( ), общий член которой задается формулой:
), общий член которой задается формулой:
 =
=  , n
, n  N.
N.
По этой формуле можно вычислить любой член последовательности:
 = 1;
= 1;  =
=  ;
;  =
=  ; …
; …
следовательно, последовательность имеет вид:
1;  ;
;  ; …;
; …;  ; …
; …
Предел последовательности
Пример:
5.10Рассмотрим последовательность с общим членом  =
=  .
.
Значения членов последовательности по мере возрастания номера n располагаются как угодно близко к 3.
Каким должно быть n, чтобы модуль разности  - 3 был меньше 0,001,
- 3 был меньше 0,001, 

(½  - 3½< 0,001)?
- 3½< 0,001)?
Выполним преобразования:
½  - 3½ = ½
- 3½ = ½  ½= ½-
½= ½-  ½=
½=  .
.
Тогда неравенство
½  -3½< 0,001 Û
-3½< 0,001 Û  < 0,001
< 0,001
справедливо для любого n > N = 1000.
Таким образом, для любого положительного числа 0,001 нашли такое натуральное число N=1000, что для любого n > N выполняется неравенство
½  - 3½< 0,001.
- 3½< 0,001.
В этом случае число 3 называется пределом последовательности ( ). Записывают так:
). Записывают так:

 =3, или
=3, или  ® 3 при n ® ¥.
® 3 при n ® ¥.
Сформулируем определение предела последовательности.
Число А называется пределом последовательности ( ), если для любого положительного числа e найдется такое натуральное число
), если для любого положительного числа e найдется такое натуральное число
N = N(e) (N зависит от e), что для любого n > N выполняется неравенство:
½  - А½< e.
- А½< e.
Записывают так:

 = А, или
= А, или  ® А при n ® ¥.
® А при n ® ¥.
Говорят:” Последовательность ( ) имеет пределом число А при n стремящемся к бесконечности” или “ последовательность (
) имеет пределом число А при n стремящемся к бесконечности” или “ последовательность ( ) сходится к числу А “.
) сходится к числу А “.
Проще: предел последовательности!{ а n} есть число А, к которому можно приблизиться с любой степенью точности при стремлении номера члена последовательности к бесконечности.
Предел функции
По аналогии с определением предела последовательности при n ® ¥ введем сначала определение предела функции при х® ¥.
Число b называется пределом функции f(x) при х® ¥, если для любого положительного числа e найдется такое число М = М(e), что для всех ½х½> М, выполняется неравенство:
½f (x)- b½< e.
Другими словами: число b называется пределом функции при х® ¥, если при всех х, удаляющихся в бесконечность значения функции неограниченно приближаются к b.
Записывают так:  f(х) = b.
f(х) = b.
Число b называется пределом функции f(х) в точке а (или при х стремящемся к а), если для любого e > 0 существует d = d(e), зависящее от e, такое, что для всех х ¹  , удовлетворяющих неравенству ½х – а½<d, справедливо неравенство ½ f(х) - b½< e.
, удовлетворяющих неравенству ½х – а½<d, справедливо неравенство ½ f(х) - b½< e.
Другими словами: число b называется пределом функции при х® а, если при всех х, неограниченно приближающихся к а, значения функции неограниченно приближаются к b.
Записывают так:  f(х) = b.
f(х) = b.
Проще: передел функции y = f(x) при стремлении х к а есть число b, к которому приближается значение у с любой наперед заданной точностью.
Геометрическая иллюстрация.
 |
y = f (х) ½ x-a ½<d,
ß
a-d < x < a+d,
½ f(х) - b½< e,
ß
b-e < f(х) < b+e.
Рис. 5.1. Предел функции.
Можно доказать:
1) Если функция имеет конечный предел, то этот предел единственный.
2) 
 = С, С = const;
= С, С = const;
3)  х = а.
х = а.
Часто рассматриваются пределы функции, если х® а и при этом х < а:
 f(x) – предел слева;
f(x) – предел слева;
или х® а и х > а:
 f(x) – предел справа.
f(x) – предел справа.
Изучаются и другие пределы функций, например:
 f(х) = +
f(х) = +  ;
;  f(х) = -
f(х) = -  ;
;
 f(x) = +
f(x) = +  ;
;  f(x) = -
f(x) = -  ;
;
 f(х) = +
f(х) = +  и т. п.
и т. п.
Теоремы о пределах.
Пусть существуют и конечны  f(х) = А;
f(х) = А;  g(x) = В, тогда
g(x) = В, тогда
1)  (f(x)
(f(x) 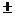 g(x)) =
g(x)) =  f(x)
f(x) 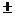
 g(x) = А
g(x) = А 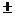 В;
В;
предел суммы (разности) функций равен сумме (разности) их пределов:
2) предел произведения функций равен произведению их пределов:
 (f(x) g(x)) = (
(f(x) g(x)) = ( f(x))(
f(x))( g(x)) = А×В;
g(x)) = А×В;
следствие: постоянный множитель можно вынести за знак предела:
 (С f(x)) = С×
(С f(x)) = С×  f(x), С = const,
f(x), С = const,
3) предел отношения двух функций равен отношению их пределов, если предел делителя отличен от нуля:

 ; В ¹ 0.
; В ¹ 0.
Пример:
5.11. Найти 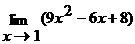 .
.
Решение. Применяя теоремы о пределах, получим:
 = =
= =  =
=
= 9×1×1-6×1+8=11
Упражнение:
5.12. Найти:  .
.
 2018-01-08
2018-01-08 451
451








