Линейные дифференциальные уравнения первого порядка называется уравнение вида
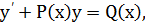
где Р(х) и Q(x) – функции от х. Если Q(x)≡0, то линейное дифференциальное уравнение называется однородным.
Пример 5. Найти общее решение уравнения 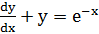 .
.
Решение. Сначала найдем общее решение линейного однородного уравнения, т.е. уравнения
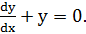 Умножив члены уравнения на
Умножив члены уравнения на 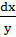 , имеем
, имеем 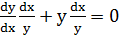 , откуда
, откуда 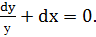
Интегрируя, получим ln|y|+x=ln|C|, откуда у=С 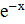 . Это и есть общее решение линейного однородного дифференциального уравнения.
. Это и есть общее решение линейного однородного дифференциального уравнения.
Будем искать общее решение заданного уравнения в виде у=С 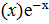 (*).
(*).
Дифференцируя равенство (*) получим 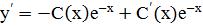 (**).
(**).
Сложив почленно левые и правые части равенств (*) и (**), найдем 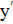 +у=
+у= 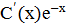 . Так как правая часть данного уравнения равна
. Так как правая часть данного уравнения равна 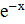 , то
, то 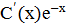 =
= 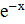 , т.е.
, т.е. 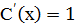 . Отсюда находим С(х) = х + С1, С – произвольная постоянная. Следовательно, искомое общее решение имеет вид
. Отсюда находим С(х) = х + С1, С – произвольная постоянная. Следовательно, искомое общее решение имеет вид 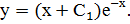
Пример 6. Найти частное решение уравнения y ' = 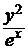 , если у = 1 при
, если у = 1 при
х = 0.
Решение. Напоминаем, что y ' = 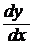 , значит
, значит 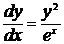 .
.
Разделяя переменные, получим: 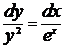
Теперь интегрируем:
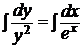 ;
; 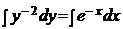 ;
;
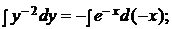
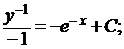
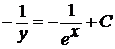 ; у =
; у = 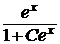 .
.
Общее решение найдено. Для нахождения значения произвольной постоянной С подставим значения х = 0 и у = 1 в общее решение:
1 = 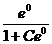 ; 1 =
; 1 = 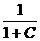 ; С = 0
; С = 0
Следовательно, искомое частное решение имеет вид у = ех
Пример 7. Решить уравнение у'=- 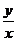 , удовлетворяющее условию у(4) = 1.
, удовлетворяющее условию у(4) = 1.
Решение. Имеем 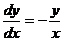 или
или 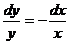 . Проинтегрировав, получим:
. Проинтегрировав, получим:
lnу=lnс-lnх, т.е. у= 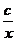 общее решение ДУ.
общее решение ДУ.
Оно представляет собой, геометрически, семейство равносторонних гипербол. Выделим среди них одну, проходящую через точку (4; 1). Подставим х = 4 и у = 1 в общее решение уравнения: 1= 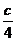 , с = 4.
, с = 4.
Получаем: у= 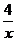 - частное решение уравнения у/=-
- частное решение уравнения у/=- 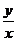
 2018-01-08
2018-01-08 359
359








