Дифференциальные уравнения первого порядка с разделяющимися переменными

Дифференциальные уравнения с разделяющимися переменными имеет вид

М₁(х)N₁(y)dx+M₂(x)N₂(y)dy=0

Поделив обе части этого уравнения на N₁(y) M₂(x), получим уравнение

в котором переменные х и у разделены. Общее решение уравнения находится почленным интегрированием:

Пример 3. Решить уравнение ху^'+у=0. Найти частное решение этого уравнения, удовлетворяющее начальному условию у=1 при х=4.

Решение. Запишем уравнение в виде у^'= или 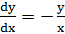. Разделив переменные, получим

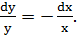Тогда , откуда ln|y|= - ln|x|+C₁, С₁ – произвольная постоянная.

Положим С₁=lnC₂; тогда ln|y|= - ln|x|+ lnC₂,откуда |y|= y=± . Так как С – произвольная постоянная, то можно считать, что ±С₂=С. Поэтому общее решение имеет вид

(*)

Геометрически общее решение (*) представляет собой множество равносторонних гипербол.

Выделим теперь из общего решения частное решение, удовлетворяющее начальному условию у(4)=1. Заменяя в равенстве (*) х и у начальными данными, получим 1=С/4, откуда С=4. Итак, искомое частное решение имеет вид у=4/х.