Катастрофи - стрибкоподібні зміни стану в динамічних системах

 

Як було сказано вище, у динамічних системах можливо не тільки гладке (безперервне) і відносно передбачуване поводження, але й різкі стрибкоподібні зміни. Такими стрибкоподібними змінами у змінних станах динамічної системи займається теорія катастроф. Хоча назва припускає дослідження подій, порівнянних зі стихійними лихами, ця теорія має справу з менш ефектною поведінкою. B рамках даної теорії розглядаються питання як технічного напрямку (перекидання судів), соціологічного (раптові спалахи агресивності, бунти), так і економічного (обвал фондового ринку).

Поводження складної динамічної системи в загальному виді може бути описано сукупністю різних інтегро-диференційних рівнянь. Однак не завжди необхідно напряму визначити повна безліч рішень, а лише потім досліджувати їхньої властивості. У багатьох випадках необхідний лише обмежений обсяг інформації якісного характеру, що дозволяє зробити висновки про поводження системи. Предметом теорії катастроф є вивчення залежності якісної природи рішень від значень параметрів, що є присутнім у заданих рівняннях.

Область дії теорії катастроф обмежена припущеннями, що спрощують, щодо системи рівнянь, що описують поводження системи.

B табл. 5.1 показані послідовні спрощення системи рівнянь, у ній y_j — змінні стани системи, t — змінна часу, x_l — просторові координати, с_а — керуючі параметри.

Отже, предметом вивчення теорії катастроф є класифікація станів рівноваги градієнтних систем, які можуть проявлятися як раптові перегони — катастрофи — у поводженні динамічної системи.

Розглянемо прапори катастроф. О наявності катастрофи свідчать спеціальні критичні крапки сімейства потенційних функцій, який описується система або явище. Однак такі крапки часто не можуть бути розпізнані відразу. Наприклад, потенційна функція є занадто складною або точно не відома. Ще гірше, коли система не є градієнтною, і зовсім погано, коли немає навіть мрячних міркувань щодо виду рівняння, що адекватно описує систему. Проте, катастрофи часто зустрічаються в реальних ситуаціях, і, отже, важливо вміти їх вчасно розпізнати. Катастрофи мають відмітні риси - прапори, які дозволяють привернути увагу до даного процесу.

Як тільки зафіксований один із цих прапорів, тобто встановлена ознака, що свідчить про наявність у системі катастрофи, управляючі параметри системи можна змінювати так, щоб виявити й інші прапори, які при відповідних умовах повинні обов'язково виявитися. Встановлення наявності й типу катастрофи у випадку невизначеності в описі системи допомагає визначити:

- спрощену модельну потенційну функцію, що залежить тільки від істотних змінних станів і керуючих параметрів;

- структурно стійку частину потенційної функції, що може підказати, який процес в дійсності має місце;

- тип рівняння для системи й те, яким образом потенційна функція в нього входить;

- непотрібність використання рівнянь взагалі.

1) Модальність.

Система може мати два або більше різних стани в деякій області зміни керуючих параметрів. Наприклад, якщо керуючі параметри системи перебувають у заштрихованій області, то система може перебувати в трьох різних станах (наприклад, катастрофа зборки на рис. 5.8).

 

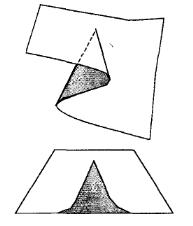
Рис. 5.8. Модальність і недосяжність у катастрофі зборки

 

2) Недосяжність.

Існує область недосяжних нестійких станів рівноваги, яким не можна прийти, рухаючись із яких-небудь стійких станів. Ha рис. 5.8 серединний шар є недосяжним.

3) Катастрофічні перегони.

Малі зміни в значеннях керуючих параметрів можуть викликати більші зміни в значеннях змінні стани системи в міру того, як система перескакує з одного локального мінімуму в іншій, перехід з околиці одного локального мінімуму в іншій проявляється у великій зміні значень зміною стану, що відбувається у надшвидкій шкалі.

 

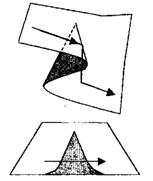
Рис. 5.9. Різкі зміни стану при гладких змінах параметрів

 

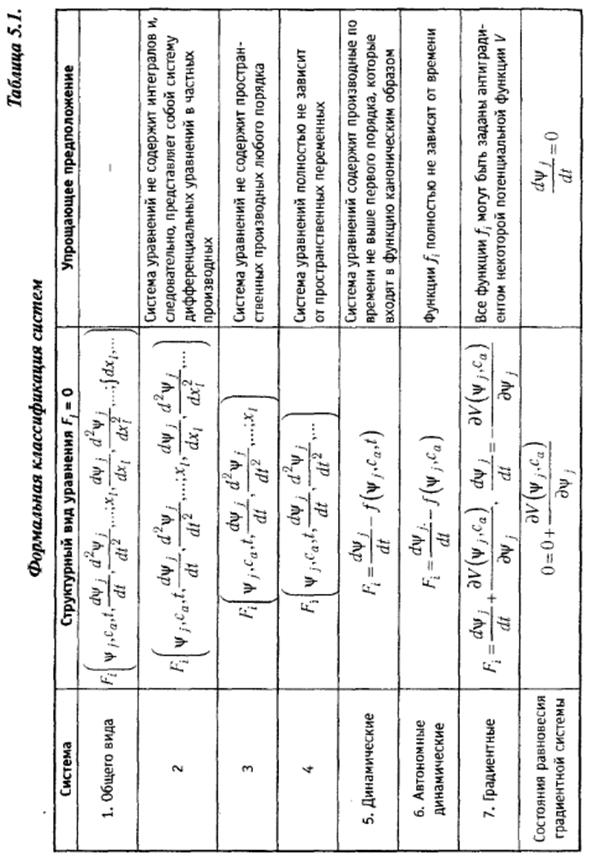
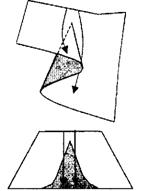
Рис. 5.10. Расходимость

 

Ha рис. 5.9 стрибок відбувається, як тільки стан системи переходить із одного шару поверхні катастрофи зборки на іншій.

Ha рис. 5.10 показано, що траєкторії зміни керуючих параметрів при близьких початкових станах системи приводять до істотного розходження кінцевих станів системи.

4) Розбіжність.

Кінцеві зміни в значенні керуючих параметрів приводять до кінцевих змін у значеннях змінні стани в крапці рівноваги. Звичайно малі зміни у вихідних значеннях керуючих параметрів ведуть лише до невеликої зміни початкових і кінцевих значень змінні стани. Однак при наявності катастрофи малі зміни початкових значень змінні стани можуть привести до більших змін кінцевих значень цих змінних.

5) Гістерезис і необоротність.

Гістерезис має місце, коли процес не є повністю оборотним. Стрибок з локального мінімуму 1 в локальний мінімум 2 може не відбутися при тих же значеннях керуючих змінних, хоча стрибок із крапки 2 у крапку 1 мав місце при русі у зворотну сторону.

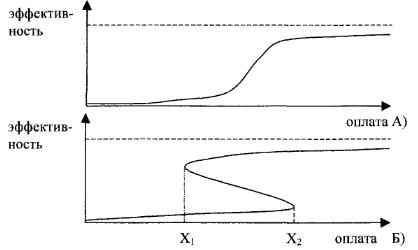
Рис. 5.11 Явище гістерезису

Якщо винагорода мала, на його думку, то працівник не буде занадто старатися. З іншої сторони, у кожного існує межа працездатності, і, як би не підвищувалася винагорода, більшого ефекту досягти не вдасться. Ця ситуація приблизно може бути описана функцією, зображеної на рис. 5.11а. Розглянемо тепер динамічний процес, у якому оплата може підвищуватися й знижуватися (рис. 5.11б). Якщо в початковий момент оплата низька, то ефективність роботи також низька. C підвищенням оплати ефективність росте, але повільно, оскільки, на думку працівника, приріст оплати недостатній для збільшення ефективності роботи. Так буде відбуватися до моменту X₂, коли подальший ріст оплати вимагає переходу на якісно новий рівень ефективності роботи. Відбувається стрибкоподібна зміна ефективності. Якщо, навпроти, у початковий момент часу оплата висока, то ефективність підтримується на високому рівні. B зменшенням оплати відбувається поступове невелике зменшення ефективності (вступає в дію деяка інерція, відповідно до якого людина продовжує працювати у звичному йому режимі). Так відбувається доти, поки оплата не досягає досить низького рівня X_l. B цей момент відбувається різке зниження ефективності, оскільки немає стимулів підтримувати її високий рівень. Фігура, зображена на рис. 5.11б, називається петлею гістерезису.

Строго говорячи, вона не є функцією, оскільки тому самому значенню X може відповідати два (або навіть три) значення Y. Наявність безлічі таких X- ï X₁; X₂ ï і приводить до можливості катастрофічних змін у стані системи. Сама безліч [ X₁;X₂ ] називається біфуркаційною безліччю, тобто таким, для значень параметрів з якого можливі кілька різних станів системи. Ha рис. 5.12 показане те ж явище в тривимірній системі.

Основними припущеннями теорії катастроф є:

1. Система є динамічної, тобто її стан змінюється в часі.

2. Принцип максимального зволікання: система прагне зберігати свій стан як можна довше.

3. Поточний стан системи залежить від того, яким образом система прийшла в цей стан.

4. Траєкторії системи необоротні, тобто при зміні керуючих параметрів системи в точності протилежним образом система не обов'язково прийде до початкового стану.

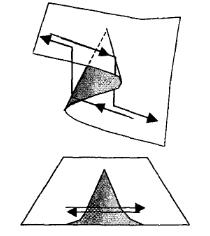
Рис. 5.12. Необоротність у трьохмірній системі

 

Катастрофою називається різка, стрибкоподібна зміна стану системи при повільній зміні її параметрів (або керуючих змінних).

Повертаючись приміром, можна помітити, що, якщо повернути осі й розглядати оплату як функцію ефективності, то ми маємо справу з поліномом третього ступеня (рис. 5.11a). Цей поліном не має экстремумов, а на мал. 5.11б має два экстремума. Очевидно, що кількість екстремальних крапок буде залежати від коефіцієнтів полінома, тобто параметрів системи.

Розглянемо локальний характер потенційних функцій. Властивості станів рівноваги залежать від виду й властивостей потенційної функції, який описується поводження системи. Раніше розглядалася класифікація станів рівноваги у двовимірних системах, де виявилися можливими 8 різних варіантів рівноваги. Якщо ж змінні стани системи більше, те повна класифікація станів рівноваги виявляється досить скрутною. Теорія катастроф дозволяє провести таку класифікацію для досить широкого класу нелінійних систем.

Розглянемо, які перетворення можливі для потенційних функцій в околиці стану рівноваги. Ці перетворення дозволяють спростити функцію й привести її к локально простому виду й виділити катастрофи.

Введемо поняття канонічної форми. Якщо в деякому стані градієнт системи відрізняється від нуля, то згідно теореми про неявну функції можливе таке перетворення координат, що потенційна функція приймає лінійний вигляд:

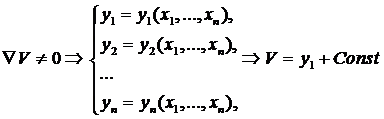(5.1)

Введемо поняття морсовської форми. Якщо розглянута система знаходиться в стані рівноваги, то градієнт функції дорівнює нулю, тому застосувати теорему про неявну функції неможливо і канонічне уявлення не має місця. Тип рівноваги виділяється власними значеннями матриці стійкості. 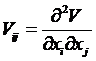Якщо визначник V_ij відрізняється від нуля, то теорема Морса гарантує існування такої гладкої заміни змінних, що потенційна функція може бути представлена квадратичною формою

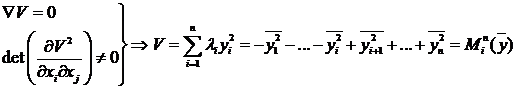(5.2)

де l_і — власні числа матриці стійкості, обчисленої в точці рівноваги.

Функцію M_іⁿ(y) називають морсовским i-сідлом. Стійкими є тільки 0-сідла.

Визначення. Критичні точки, у яких detV_ij = 0, називаються ізольованими, невиродженими, або морсовськими.

Розглянемо поняття форми Тома.

Визначення. Критичні точки, у яких detV_ij¹ 0, називаються неізольованими, виродженими, або неморсовскими. Точки (x, с) у просторі змінні стани й параметрів функції, для яких detV_ij= 0 називається множиною сингулярності.

Як треба з виду розглянутих рівнянь, безліч точок рівноваги (поверхня рівноваги) задається співвідношенням

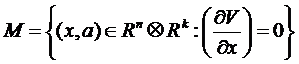(5.3)

Проекція безлічі сингулярності на параметричний простір називається біфуркаціонною безліччю:

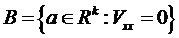(5.4)

Якщо потенційна функція залежить від одного або більше керуючих параметрів, то матриця стійкості V_ij і її власні значення також залежать від цих параметрів. B цьому випадку цілком можливо, що при деяких значеннях керуючих параметрів одне або кілька власних значень матриці стійкості можуть звернутися в нуль. Тоді й detV_ij= 0, і умови застосування леми Морсу не виконуються, отже, подання у вигляді квадратичної форми виявляється неможливо. Однак можна знайти деяке розщеплення, що дозволяє відокремити координати, що відповідають нульовим власним значенням, й інші:

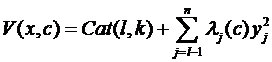, (5.5)

або, при деяких додаткових умовах,

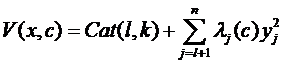, (5.6)

де Cat (l,k) – функція катастрофи.

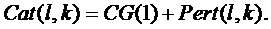(5.7)

Cat (l,k) – паросток катастрофи, Pert(l,k) – обурення, l - кількість нульових власних значень матриці стійкості.

Параметри потенційної функції визначають також кількість і характер її екстремумів. Це наочно видно, якщо розглянути поліноміальні функції виду

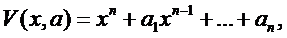(5.8)

де деякі а, можливо, дорівнюють нулю.

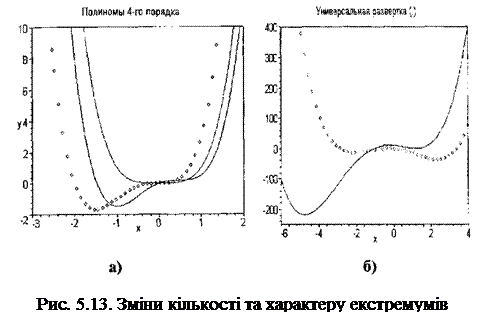Для заданого n графік многочлена має різну форму, при різних рівних нулю параметрах. На рис. 5.13 наведено графіки полінома 4-го порядку.

 

Визначення. Функція виду (5.8) з деякими а, можливо, рівними нулю називається структурно стабільної, якщо кількість і характер экстремумів цієї функції не міняється, коли деякі із цих ai міняють значення. Ця структурно стабільна форма полінома для заданого ступеня n називається універсальним розгорненням для хⁿ. Кількість відмінних від нуля параметрів, які необхідні, щоб стабілізувати хⁿ, називається домірністю розгорнення.

Наприклад, функція f(x)=x⁴ не є структурно стабільною, оскільки f(x)=x4+а1x³ має додатковий экстремум. На мал. 5.13 наведений графік універсального розгорнення для x⁴ і повного поліному 4-го ступеня виду (5.8). Універсальним розгорненням для x⁴ є h(x)=x⁴ + а2х² + а3х.

Універсальні розгорнення поліномів і являють собою функції катастроф у розкладанні потенційної функції рівнянь, що описують систему.

Опис і характеристика елементарних катастроф Тома при одному або двум нульовим власним значенням із числом параметрів не більше 5 даний у табл. 5.2.

Таблиця 5.2

Елементарні катастрофи

Тип катастрофи	Кількість керуючих параметрів	Паросток катастрофи	Збурювання
Складка		x3	a1x
Збірка		±х4	a1x2 + а2х
Ластівчин хвіст		x5	a1x3 + а2х2 + а3х
Метелик		±х6	a1x4 + а2х3+а3х2+а4х
Вігвам		x7	a1x5 + a2x4 + а3х3+ a4x2 + а5х
D-4		х2y - y3	a1x + а2у + а3y2
D+4		х2y + y3	a1x + а2у + а3y2
D5		х2y + y4	a1y2 + а2х2 + а3y + а4х
D-6		х2y - y5	a1y3 + а2y2 + а3х2+ а4y + а5х
D+6		х2y + y5	a1y3 + a2y2+ а3х2 + a4y + а5х
E±6		х3±у4	a1xy2 + а2y2 + а3ху + а4y + a5x

 

Приклад 5.3. Припустимо, що потенційна функція залежить від десяти змінних стану й трьох керуючих параметрів. Нехай крапка (х0, с0) -неморсовська критична крапка, у якій матриця стійкості має два нульових власних значення (дефект 2), три негативних і п'ять позитивних власних значення. Визначимо локальний характер цієї функції.

Згідно розкладенню Тома маємо:

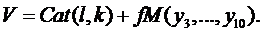
Оскільки l=2, k=3, з табл. 5.2 знаходимо, що має місце катастрофа виду D±4, тобто

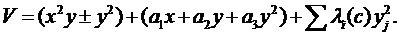
Розглянемо питання щодо геометрії складки і збірки.

Приклад 5.4. Розглянемо катастрофу складки: V(x,a)=x³ + ax.

Дана функція при а < 0 має дві критичні крапки, при а=0 - одну двічі виражену критичну крапку, а при а > 0 не має ні однієї критичної крапки (Рис 5.14). Її поверхня рівноваги M: 3х²+а=0 існує лише при від’ємних значеннях параметра.

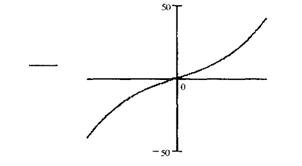
Рис. 5.14. Потенційна функція для катастрофи складки

 

Множина сингулярності визначається співвідношенням 6x=0, отже, вона складається з єдиної крапки x=0. Біфуркація (роздвоєння) поводження відбувається при а=0. При негативних значеннях параметра існують галузі стійкої й хиткої рівноваги. Критичні крапки функції визначаються зі співвідношення (рис. 5.15):

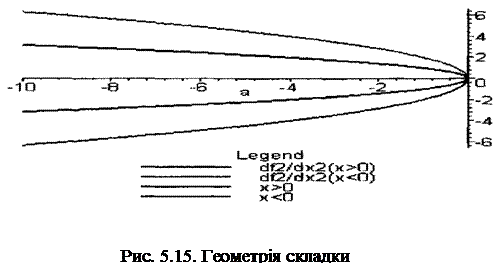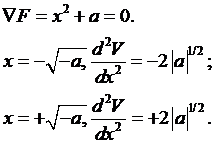
Приклад 5.5. Розглянемо катастрофу збірки (крапка повернення). Вона задається потенційною функцією виду

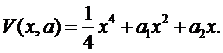
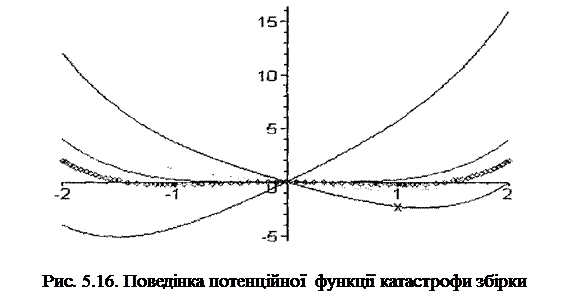
Будь-яка крапка простору параметрів (a1, а2) за винятком крапок сепаратриси забезпечує існування однієї або трьох ізольованих критичних крапок. На рис. 5.16 представлені графіки функції при різних сполученнях параметрів. Усередині області, що має форму збірки, V(x, a1, а2) має три ізольовані критичні крапки, а поза цією областю — усього одну; на границі функція має одну ізольовану критичну крапку й одну двічі виражену, а на початку координат — одну тричі виражену критичну крапку.

Поверхня рівноваги визначається співвідношенням:

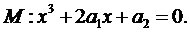
Множина сингулярності: S: 3x²+2a1=0.

Виключивши із рівнянь для M і S змінну x, одержуємо біфуркаційну множину:

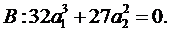
На рис. 5.17 показана поверхня рівноваги й біфуркаційна множина катастрофи збірки.

		Рис. 5.17. Катастрофа збірки

Рис. 5.17. Катастрофа збірки

 

Як видно з малюнка, система, що починає свій рух з точки А, буде як можна довше рухатися по верхній частині поверхні, поки не досягне множини сингулярності в крапці В. Потім система робить різкий стрибок униз у крапку C і далі буде рухатися по нижній частині поверхні. Якщо система починає свій рух на нижній частині, то вона перетне біфуркацвйну множини у крапці D і зробить різкий стрибок на верхню частину поверхні. Можливо й інше поводження системи, що не включає різких переходів. Наприклад, по траєкторії FG, якщо один з параметрів системи також може швидко змінюватися.

Економічні додатки теорії катастроф багато в чому опираються на геометричні аспекти, в основному для опису економічного поводження застосовується саме катастрофа зборки. Інші елементарні катастрофи проілюструвати складно, оскільки в них необхідне закріплення одного або декількох параметрів.

Теорія катастроф застосовується для вивчення багатьох проблем, включаючи крах фондових бірж, поводження уряду, макромоделі, структурні аспекти припущення Вальраса й ін.