Лекция 2. Действия с комплексными числами в алгебраической форме

2.1. Действия

Рассматриваем числа:

 

1) Сложение: формула (1) Свойства сложения: а) коммутативность б) ассоциативность:

 

2) Вычитание: формула (2)

 

 

3) Умножение: формула (3) Свойства умножения: а) коммутативность; б) ассоциативность;

в) дистрибутивность:

На самом деле, можно умножать каждое слагаемое одной скобки на каждое слагаемое другой. Так бывает проще.

Выполним рассмотренные действия для двух заданных комплексных чисел:

Пусть:

 

1) ;

2) ;

3) или

 

Теперь, самостоятельно для чисел: выполните те же действия.

 

4) Деление: частным комплексных чисел является комплексное число , удовлетворяющее условию: или .

Тогда, чтобы найти число z, необходимо решить систему уравнений:

Пример:

 

Операция долгая, неудобная, поэтому: введем число комплексно сопряженное числу

При этом:

1)

2)

3) для любых комплексных чисел, отличных от нуля.

Тогда, удобно при делении избавляться от мнимости в знаменателе путем домножения числителя и знаменателя на число сопряженное знаменателю.

Пример: (тот же пример)

Фактически операция деления комплексных чисел заменяется операцией умножения на обратное число:

Для любого комплексного числа - обратное число. При этом

Пример: . Найти обратное число:

Введение обратного числа необходимо и для операции 5.

 

5) Возведение в степень:

Правила

 

2.2. Практическая работа № 1 «Действия с комплексными числами в алгебраической форме»

1) Посчитаем степени числа :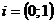

 

2) Вычислить:

2.1) ; 2.2) ;

2.3) ;

2.4) ;

2.5) ;

3) Найти решение уравнения:

Решение:

4) Вычислить:

4.1)

4.2)

4.3)

4.4)

4.5)

5) Вычислить: а) число , если ; б) число

Решение:

а)

б)