Числовая последовательность

Последовательность можно понимать как частный вид функций, а именно как функцию номера места члена последовательности 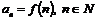. Обозначение числовой последовательности - или , где n – номер члена последовательности, a_n – общий член последовательности.

S_n – последовательность сумм. .

Примеры числовых последовательностей:

• ;
• ;
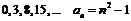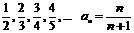• и т.д.

Способ задания последовательности, при котором для вычисления n-го члена надо знать предыдущие, называется рекуррентным.

1.4.2. Основные элементарные функции

· Степенная: ;

· Рациональная (это комбинация степенных с коэффициентами): ;

· Показательная: ;

· Логарифмическая: ;

· Тригонометрические: ;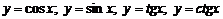

· Обратные тригонометрические: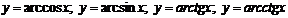

1.4.3. Сложная функция

Это функция, аргументом которой тоже является функция.

Пусть u = g(x) – функция, определенная на множестве D(u) и со значениями E(u),

y = f(u) – функция, определенная на множестве E(u). Тогда каждому xÎD(u) можно поставить в соответствие: x ——^g—> g(x) ——^f—> f(g(x))

Тогда 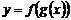– сложная функция (или композиция функций f ○ g).

При этом u = g(x) – внутренняя функция, y = f(u) – внешняя функция.

Например: 1) y = (3x – 5)⁵ u = 3x – 5 – внутренняя, y = u⁵ – внешняя

2) y = cos(1 – x²) u = 1 – x² – внутренняя, y = cos u – внешняя.

Обратная функция

Чтобы функция имела обратную, она должна быть обратимой.

Функция y = f(x) с областью определения A и множеством значений B называется обратимой, если для любых x₁, x₂ Î A (x₁ ≠ x₂) выполняется условие f(x₁) ≠ f(x₂).

Примеры обратных функций:

1) Для функции - обратная функция;

2) Функция необратима на множестве (- ∞; ∞), но обратима на множестве .

Графики взаимно обратных функций симметричны относительно прямой y = x (биссектрисы первой и третьей четвертей).

Композиция двух взаимно обратных функций всегда равна аргументу. Например: