2018-01-08
2309
Существует несколько стандартных методов вычисления интегралов. Непосредственное интегрирование подразумевает вычисление неопределенного интеграла только при помощи свойств интеграла и таблицы основных интегралов.
Примеры. Вычислить интегралы:
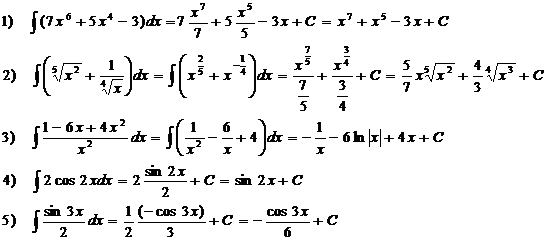
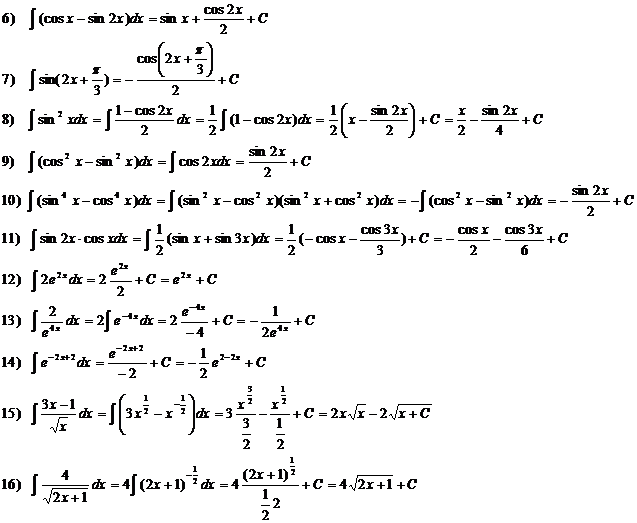
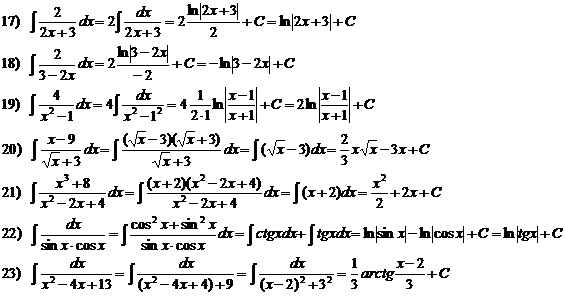
В примере № 20 использована операция «домножения на сопряженное», в примере № 23 – метод выделения полного квадрата:
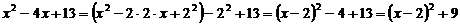
Домашнее задание № 9 «Непосредственное интегрирование»
Вычислить интегралы:
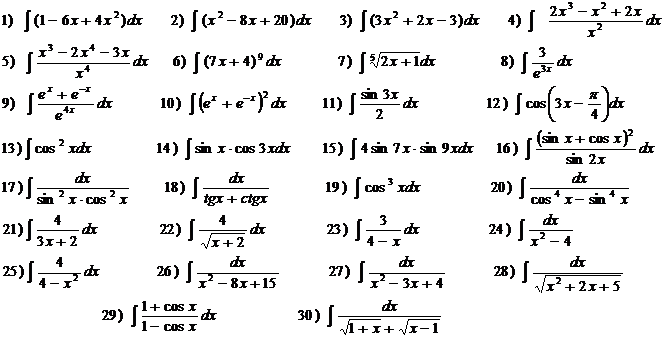
Лекция 3. Методы интегрирования. Метод подстановки
3.1. Интегрирование методом замены переменной (метод подстановки)
Если не удается найти интеграл непосредственно, то интегрируем методом подстановки.
Сущность метода: введением новой переменной интегрирования свести заданный интеграл к новому, который вычисляется непосредственно.
При этом должен остаться интеграл, в котором будет только одна переменная. Для этого обозначаем вводимую переменную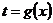 
и считаем 
. После интегрирования необходимо вернуться к исходной переменной.
|
|
|
Пример оформления:
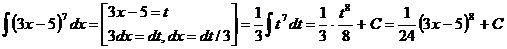
3.2. Практическая работа № 8 «Методы интегрирования»
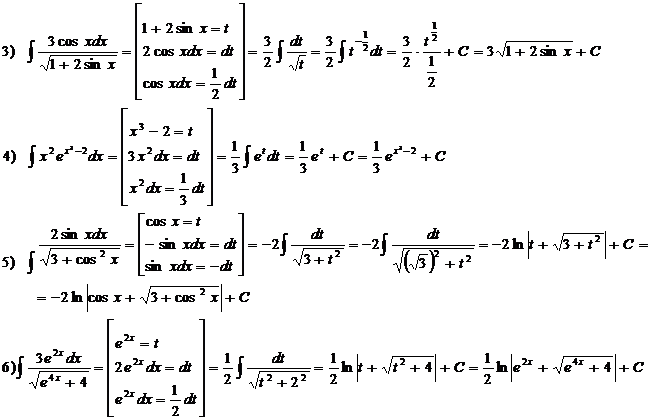
В примере № 7 воспользуемся методом выделения полного квадрата, чтобы свести интеграл к табличному.
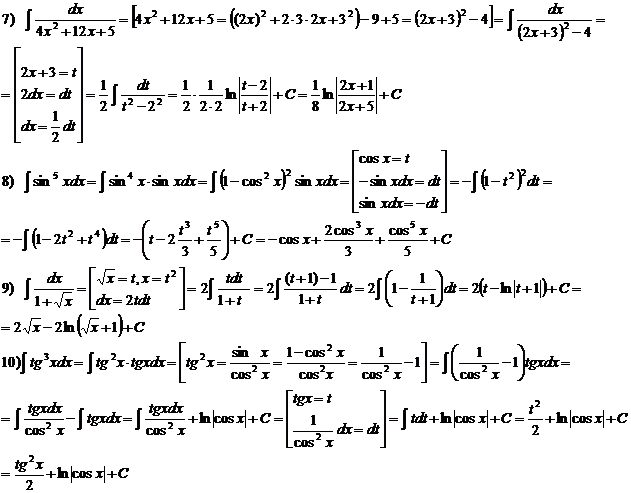
Домашнее задание № 10 «Интегрирование методом подстановки»
Вычислить интегралы:
А)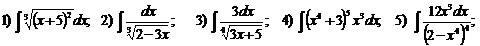 
Б)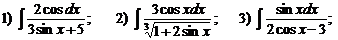 
В)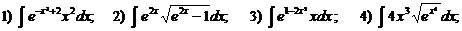 
Г) 
Д)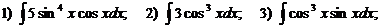 
Е)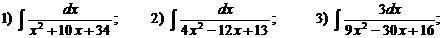 
Ж)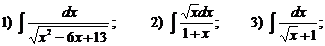 
З)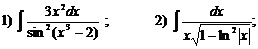 
Ответы:
А): 
Б): 
В):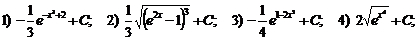 
Г):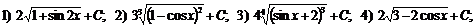 
Д):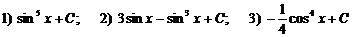 
Е):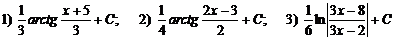 
Ж):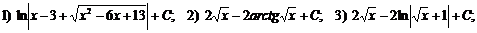 
З): 
