Рекомендации к решению заданий. Для решения заданий 5 – 7 необходимо знать правила дифференцирования и таблицу производных основных элементарных функций

 

Для решения заданий 5 – 7 необходимо знать правила дифференцирования и таблицу производных основных элементарных функций.

Правила дифференцирования:

1. ;	2. ;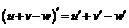
3. ;	4. .

Производные основных элементарных функций:

1.	;	.
2.	;	.
3.	;	.
4.	;	.
5.	;	.
6.	;	.
7.	;	.
8.	;	.
9.	;	.
10.	;	.
11.	;	.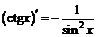
12.	;	.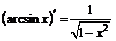
13.	;	.
14.	;	.
15.	;	.

 

В левом столбце приведенной выше таблицы записаны производные основных элементарных функций, в правом – производные соответствующих сложных функций.

 

Найдем производные заданных функций.

1. .

+ .

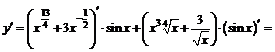
2. .

.

3. .

.

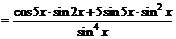4. .

.

 

Задание 5

 

Задачи 81–100. Найти производные заданных функций.

 

81.	;	;
	;	.
82.	;	;
	;	.
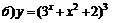83.	;	;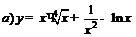
	;	.
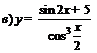84.		;
	;	.
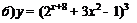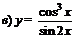85.	;	;
	;	.
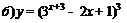86.	;	;
	;	.
87.		;
	;	.
88.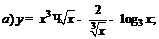
89.	;	;
	;	.
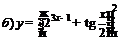90.	;	;
	;	.
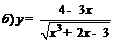91.	;	;
	;	.
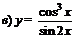92.	;	;
	;	.
93.	;	;
	;	.
94.	;	;
	;	.
95.	;	;
	;	.
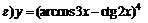96.	;	;
	;	.
97.		;
	;	.
98.	;	;
	;	.
99.	;	;
	;	.
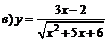100.	;	;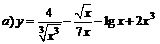
	;	.

 

Пусть требуется провести полное исследование функции и построить ее график.

 

1. Область определения функции характеризуется неравенством х +4¹0, откуда получаем х ¹–4, т. е.

2. Исследуем функцию на непрерывность. Из пункта 1 следует, что функция не определена в точке x = –4. Значит, эта точка является точкой разрыва графика функции. Классифицируем данный разрыв. Для этого вычислим односторонние пределы функции в этой точке:

, .

Таким образом, точка является точкой разрыва второго рода, а прямая – вертикальной асимптотой графика функции.

3. Исследуем функцию на наличие наклонных асимптот:

.

.

Так как оба предела существуют и конечны, то прямая y=3 x –10 является наклонной асимптотой графика функции.

4. Функция имеет общий вид, так как область ее определения не симметрична относительно начала координат.

5. Исследуем функцию на экстремум. Для этого найдем критические точки – это точки, в которых первая производная функции обращается в ноль или не существует. Первая производная функции будет равна:

 

Приравняем ее к нулю: 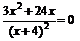. Решим полученное уравнение. Данное уравнение равно нулю, когда числитель равен нулю: . В результате получаем критические точки .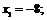

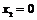Разобьем область определения критическими точками на интервалы и определим знаки первой производной на каждом интервале:

 

x	(-¥; –8)	–8	(–8; –4)	–4	(–4; 0)		(0; +¥)
y¢	+		–	Не сущ.	–		+
y		max – 46		Не сущ.		min

 

y _max= y (–8)= – 46; y _min= y (0)=2.

 

 

6. Исследуем функцию на перегиб. Для этого найдем точки подозрительные на перегиб:

 

=

.

 

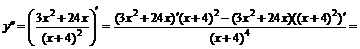
Так как вторая производная функции никогда в ноль не обращается, то график заданной функции точек перегиба не имеет.

Покажем интервалы выпуклости вверх и вниз для данной функции. Для этого рассмотрим интервалы области определения функции и определим знак ее второй производной на этих интервалах.

 

 

х (–¥; –4) –4 (–4; +¥) y ² – Не сущ. + y Ç Не сущ. È

 

 

Анализ показывает, что на интервале (–¥; –4) график функции является выпуклым вверх, а на интервале (–4; +¥) – выпуклым вниз.

7. По результатам исследования стро­им график функции (рис. 2).

Задание 6

 

Задачи 101–120. Провести полное исследование функций и построить графики:

 

101. .	111. .
102. .	112. .
103. 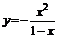.	113. .
104. .	114. .
105. .	115. .
106. .	116. .
107. .	117. .
108. .	118. .
109. 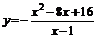.	119. .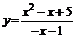
110.	120. .

Пусть задана функция S (t) = 7 t ⁴–3 t ³+2 t ²–5 t +6, которая определяет перемещение материальной точки. Требуется найти значения скорости и ускорения этой точки в момент времени t ₀=1.

Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются значениями соответственно первой и второй производной функции, определяющей ее перемещение, в этот момент времени. Поэтому найдем:

;

.

 

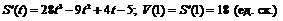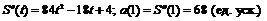Задание 7

 

Задачи 121–140. В задачах задан закон S (t) перемещения материальной точки. Требуется найти значения скорости и ускорения этой точки в момент времени t ₀.

121. S (t)=3 t 4+2 t 2– t +1, t 0=1.	122. S (t)= t 4+ t 2–5 t +1, t 0=2.
123. S (t)=4 t 4–2 t 3+ t 2–3, t 0=1.	124. S(t)=2 t 4–5 t 3+11 t 2+22 t –1, t 0=2.
125. S(t)=3 t 4–2 t 3+7 t 2+ t –1, t 0=1.	126. S (t)=4 t 4–8 t 3+5 t 2+2 t +3, t 0=2.
127. S (t)=2 t 4– t 3+3 t 2–5 t +1, t 0=1.	128. S (t)=3 t 4+2 t 3– t 2+4 t, t 0=2.
129. S (t)=2 t 4–7 t 3+5 t 2– t +2, t 0=1.	130. S (t)=5 t 4–3 t 3+2 t 2+2 t –7, t 0=1.
131. S (t)= t 4–2 t 3+6 t 2–3 t +1, t 0=1.	132. S (t)=3 t 4–5 t 3+ t 2–7 t +3, t 0=2.
133. S (t)=2 t 4+3 t 3+ t 2–5 t +11, t 0=1.	134. S (t)=4 t 4–5 t 2+5 t +3, t 0=2.
135. S (t)=2 t 4–3 t 3+4 t –1, t 0=1.	136. S (t)=5 t 4–7 t 3+ t 2–3, t 0=2.
137. S (t)=5 t 4+8 t 3–2 t 2+t–1, t 0=1.	138. S (t)=3 t 4+2 t 2–3, t 0=2.
139. S (t)=2 t 4–3 t 2+6 t –1, t 0=1.	140. S (t)=3 t 4–4 t 3+2 t 2– t +6, t 0=2.

 

Тема 6. нЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

 

Вопросы для самопроверки

 

1. Сформулируйте определение первообразной функции.

2. Что называется неопределенным интегралом функции?

3. Какое действие называют интегрированием функции?

4. Сформулируйте основные правила интегрирования.

5. Укажите основные свойства неопределенного интеграла.

6. Запишите формулу интегрирования по частям и изложите идею этого метода.

7. Укажите типы интегралов, в которых используется метод интегрирования по частям. Как использовать его в этих интегралах?