Описание установки и методика измерения
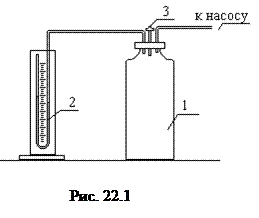 Экспериментальная установка (рис. 22.1) состоит из стеклянного баллона 1 соединенного с открытым U-образным водяным манометром 2 и имеющего кран 3. Кран позволяет баллону сообщаться с атмосферой. К баллону подсоединен нагнетательный воздушный насос.
Экспериментальная установка (рис. 22.1) состоит из стеклянного баллона 1 соединенного с открытым U-образным водяным манометром 2 и имеющего кран 3. Кран позволяет баллону сообщаться с атмосферой. К баллону подсоединен нагнетательный воздушный насос.
В работе определение отношения 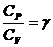 производится классическим методом Клемана и Дезорма, основанным на использовании уравнения изотермического процесса
производится классическим методом Клемана и Дезорма, основанным на использовании уравнения изотермического процесса
 (22.10)
(22.10)
и уравнения адиабатического процесса
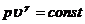 (22.11)
(22.11)
соблюдающихся для идеального газа.
В равенствах (22.10) и (22.11)  обозначает по прежнему давление, а
обозначает по прежнему давление, а 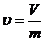 - удельный объем газа.
- удельный объем газа.
Исследуются параметры идеального газа, последовательно проходящего через три состояния. Вначале с помощью насоса необходимо по возможности быстро накачать небольшое количество воздуха в баллон при закрытом кране 3. Через 2-3 мин. температура воздуха в баллоне понизится до температуры окружающей среды 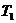 , газ придет в состояние равновесия. Об этом можно судить по прекращению изменений показаний манометра. В этих условиях берется отсчет разности уровней
, газ придет в состояние равновесия. Об этом можно судить по прекращению изменений показаний манометра. В этих условиях берется отсчет разности уровней  в обоих коленах манометра. Обозначим для первого данного состояния газа его удельный объем
в обоих коленах манометра. Обозначим для первого данного состояния газа его удельный объем  , давление
, давление 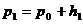 , температуру
, температуру 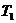 (
(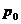 - атмосферное давлении,
- атмосферное давлении, 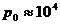 мм водяного столба).
мм водяного столба).
Если теперь открыть кран 3 быстро, на несколько секунд, то баллон соединяется с атмосферой. Практически сразу давление воздуха в баллоне станет равным атмосферному 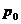 . Процесс происходит быстро и его можно считать адиабатическим. При адиабатическом расширении газ охлаждается до температуры
. Процесс происходит быстро и его можно считать адиабатическим. При адиабатическом расширении газ охлаждается до температуры 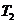 . Второе состояние газа характеризуется параметрами:
. Второе состояние газа характеризуется параметрами:  - новый удельный объем,
- новый удельный объем, 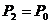 атмосферное давление и
атмосферное давление и 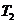 - температура (
- температура (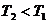 ).
).
Затем кран 3 закрыть. Давление газа в баллоне начнет возрастать, так как охладившийся при адиабатическом расширении воздух станет снова нагреваться. Воздух нагревается изохорически до комнатной температуры 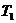 . Возрастание давления – изменение положения уровней в манометре прекратится, когда установится новое равновесное состояние газа, которому соответствует разность уровней в манометре
. Возрастание давления – изменение положения уровней в манометре прекратится, когда установится новое равновесное состояние газа, которому соответствует разность уровней в манометре 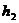 . Параметры газа в этом третьем состоянии: давление
. Параметры газа в этом третьем состоянии: давление 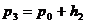 , удельный объем
, удельный объем 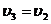 (ни масса, ни объем газа при последних изменениях не менялись), температура
(ни масса, ни объем газа при последних изменениях не менялись), температура 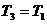 .
.
На рис.22.2 показаны адиабата (1-2) и изохора (2-3). Состояние газа 1 и 3 имеют одну и ту же температуру 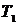 . Следовательно, точки 1 и 3 должны находиться на одной изотерме (1-3).
. Следовательно, точки 1 и 3 должны находиться на одной изотерме (1-3).
Переход (1-2) из первого состояния во второе описывается уравнением Пуассона (22.9), которое в нашем случае следует записать так:
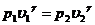 или
или 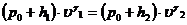 (22.12)
(22.12)
здесь  и
и 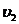 - удельные объемы газа до и после расширения.
- удельные объемы газа до и после расширения.
Сравнивая конечное, третье состояние с первым, видим, что температура газа в этих состояниях одинакова. Значит, к переходу (1-3) применим закон Бойля – Мариотта.
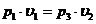 или
или 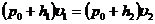 (22.13)
(22.13)
Возведя полученное равенство (22.13) в степень  , разделив его на (22.12) и прологарифмировав полученное выражение, приходим к формуле
, разделив его на (22.12) и прологарифмировав полученное выражение, приходим к формуле
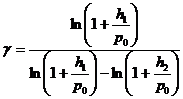 (22.14)
(22.14)
Так как 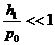 и
и 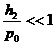 , то можно воспользоваться приближенной формулой
, то можно воспользоваться приближенной формулой 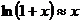 и записать (22.14) в виде
и записать (22.14) в виде
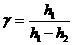 (22.15)
(22.15)
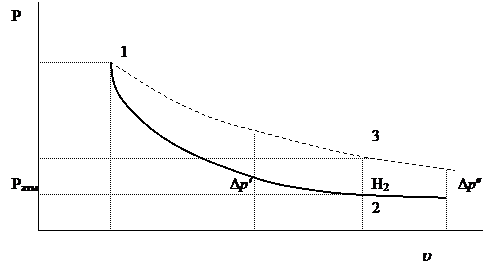
Рис. 22.2
Необходимо отметить, что на опыте не удается осуществить совпадение момента перекрытия крана с окончанием адиабатического расширения (состояние 2). Если кран закрыть раньше, чем давление упадет до атмосферного (на рис 22.2 пунктирная линия; в нашем случае 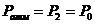 ), то получим завышенное значение
), то получим завышенное значение 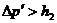 . Наоборот, при запаздывании получается заниженное значение
. Наоборот, при запаздывании получается заниженное значение 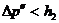 и чем больше время запаздывания
и чем больше время запаздывания 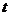 , тем сильнее
, тем сильнее 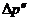 отличается от равновесного значения
отличается от равновесного значения 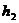 .
.
Адиабатический переход газа из состояния 1 в состоянии 2 происходит за какое-то время 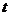 . Величина
. Величина 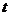 неизвестна. Однако это время гораздо меньше чем время, в течение которого необходимо держать кран в открытом положении. Поэтому время запаздывания
неизвестна. Однако это время гораздо меньше чем время, в течение которого необходимо держать кран в открытом положении. Поэтому время запаздывания 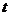 можно считать равным полному времени открытия крана. Как показывает опыт, величины
можно считать равным полному времени открытия крана. Как показывает опыт, величины 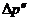 ,
, 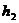 и
и 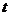 связаны следующим соотношением
связаны следующим соотношением
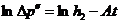 (22.16)
(22.16)
где 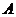 - константа.
- константа.
Из (22.16) следует, что истинное значение  можно найти из графика зависимости
можно найти из графика зависимости 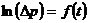 , продолжив его до точки пересечения с осью ординат, т.е.
, продолжив его до точки пересечения с осью ординат, т.е. 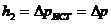 при
при 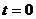 .
.
 2018-01-08
2018-01-08 1184
1184








