Приклад виконання завдання. 1. Розв’яжемо задачу при N = 3, p = 0,8

1. Розв’яжемо задачу при N = 3, p = 0,8.

а) Дискретна випадкова величина 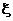- число випробуваних приладів. Можливі значення цієї випадкової величини: Знайдемо ймовірності цих значень. Позначимо події: - i-ий випробуваний прилад виявився надійним, - i-ий випробуваний прилад виявився ненадійним. Тоді

= P(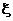 =1) = P() = 1- 0,8 = 0,2,

= P(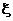 =2) = P() = 0,8· 0,2 =0,16,

= P(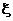 =3) = P() = 0,8·0,8·0,2 + 0,8· 0,8·0,8 = 0,64.

Закон розподілу має вигляд (Таблиця 2):

Таблиця 2. Закон розподілу дискретної випадкової величини.


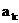
	0,2	0,16	0,64

б) Функцією розподілу F(x), яка визначена для будь-якого дійсного x, називається ймовірність того, що випадкова величина x прийме значення менше x, тобто де 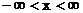. Оскільки функція F(x) визначена для всіх дійсних значень x, то розглянемо послідовно інтервали:

1) х Î (- ∞, 1], F (x) = P (x < x) = 0, тому що подія(x < x)для такого x єнеможливою подією.

2) х Î (1, 2], F (x) = P(x = 1) = 0,2, тут нерівності x < x задовольняє єдине значення x= 1

3) х Î (2, 3], F (x) = P(x = 1) + P (x = 2) = 0,2 + 0,16 = 0,36, тут нерівності x < x задовольняють два значення x = 1і x = 2.

4) xÎ (3, 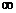), F (x) = P(x = 1) + P (x = 2) + P (x = 3) = 0,2 + 0,16 + 0,64 = 1, тут нерівності x < x задовольняють всі значення x. Таким чином,

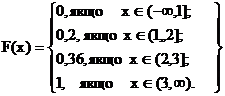
График функції розподілу наведен на Рисунку 1.

Рисунок 1. Графік розподілу випадкової величини Задачи 1..

в) Знайдемо математичне сподівання та дисперсію.

=1· 0,2 + 2 · 0,16 + 3 · 0,64 = 2,44,

1· 0,2 + 4 · 0,16 + 9 · 0,64 - (2,44)²= 0,6464.

2. Випадкова величина розподілена за законом, який обумовлений щільністю розподілу ймовірностей виду

f (x) =

Знайти параметр a, F(x), M (x), D ( x).

Параметр a знайдемо із властивості , інтеграл розіб'ємо на суму трьох інтегралів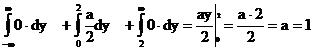

Намалюємо графік щільності розподілу f (x) (Рисунок 2)

Рисунок 2. Графік щільності розподілу f (x)

Обчислимо функцію розподілу, для цього розглянемо інтервали .

1. х Î (- ∞, 0) ,

2. х Î [0, 2] ,

3. х (2, ) .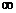

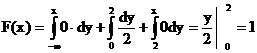Графік функції наведений на Рисунку 3.

Обчислимо математичне сподівання й дисперсію:

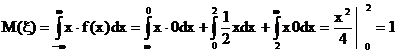
Рисунок 3. Графік функції розподілу неперервної випадкової величини.

Варіанти завдань.

Таблиця 3. Варіанти до завдання 2.

Пере- мінна	Номер варіанта

N
p	0,80	0,82	0,83	0,84	0,85	0,96	0,97	8,88	0,90	0,91	0,92	0,93	0,94	0,95	0,96
k
x₁	-1	-1,5	-2	-2,5	-1	-1.5	-2						1,5	1,5	-1,5
x₂									1,5		2,5			2,5	1,5

Продовження Таблиці 3.

Пере- мінна	Номер варіанта

N
p	0,80	0,82	0,83	0,84	0,85	0,96	0,97	8,88	0,90	0,91	0,92	0,93	0,94	0,95	0,96
k
x₁	-0,5	-0,5	-0,5	-1	-0,2	-0,2	-0,2	-1,2	-1,2	-1,2	-1,2	-0.8	-0,8	-0,7	-0,7
x₂	0,5		1,5		0,2	0,5		1,2	1,5	0,5	0,2		0,5	0,7	1,5

Тема 3. Граничні теореми.

Завдання 3

Ціль завдання – навчитися обчислювати ймовірності появи події А при великому числі n незалежних випробувань. Придбати навички у використанні таблиці для функції Лапласа.

Завдання містить одну задачу. Варіанти наведені в Таблиці 4.

Завдання № 1. Відділ технічного контролю перевіряє якість навмання відібраних n виробів. Імовірність того, що деталь задовольняє вимогам стандарту, дорівнює р. Знайти ймовірність того, що серед відібраних виробів виявиться:

а) m некондиційних;

б) не більш, ніж m₁ некондиційних;

в) від m₁ до m₂ некондиційних.