Тема 1. Випадкові події. Класичне означення ймовірності.
Теореми теорії ймовірностей.
Завдання № 1
Ціль завдання – закріплення знань основних понять теорії ймовірностей (випадковий експеримент, випадкова подія, ймовірність появи випадкової події). Придбання вмінь і навичок у виконанні операцій над подіями й у підрахунку ймовірностей настання випадкових подій. Завдання містить чотири задачі. Варіанти наведені в Таблиці 1.
Задача 1. У партії з s виробів r - бракованих. Визначити ймовірність того, що серед обраних навмання для перевірки g виробів виявляться бракованими:
а) рівно h виробів;
б) не більше h виробів.
Задача 2. У збиральний цех заводу надходять деталі із трьох автоматів. Перший автомат дає 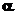 % браку, другий -
% браку, другий -  %, третій -
%, третій -  %. Визначити ймовірність влучення на зборку не бракованої деталі, якщо з кожного автомата в цех надійшло відповідно L, M, N деталей.
%. Визначити ймовірність влучення на зборку не бракованої деталі, якщо з кожного автомата в цех надійшло відповідно L, M, N деталей.
Задача 3. У збиральний цех заводу надходять деталі із трьох автоматів. Перший автомат дає 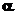 % браку, другий -
% браку, другий -  %, третій -
%, третій -  %. З кожного автомата надійшло на зборку відповідно L, M, N деталей. Узята на зборку деталь виявилася бракованою. Знайти ймовірність того, що деталь надійшла з 1-го автомата.
%. З кожного автомата надійшло на зборку відповідно L, M, N деталей. Узята на зборку деталь виявилася бракованою. Знайти ймовірність того, що деталь надійшла з 1-го автомата.
Задача 4. Робітник обслуговує a верстатів. Ймовірність виходу верстата з ладу за зміну дорівнює p. Яка ймовірність того, що робітникові прийде ремонтувати c верстатів? Яке найімовірніше число верстатів, що вимагають ремонту за зміну?
Приклад виконання завдання.
1. У ящику перебуває 10 деталей, серед яких 3 бракованих. З ящика навмання витягають 5 деталей. Знайти ймовірність того, що серед них виявиться:
а) дві браковані;
б) не більше одного бракованого;
в) хоча б одне браковане.
Розв’язання. а) Подія А - серед 5-ти витягнутих деталей 2 бракованих, а три доброякісних.
Для підрахунку m і n використаємо правило сполучень:
n =  , P(A) =
, P(A) =  =
=  =
= 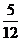 .
.
б) Нехай подія А - серед обраних виробів не більше одного бракованого,
Розглянемо події: А  - серед обраних виробів - жодного бракованого,
- серед обраних виробів - жодного бракованого,
А  - серед обраних виробів - один бракований.
- серед обраних виробів - один бракований.
Тоді А = А  + А
+ А  , причому А
, причому А  , А
, А  - несумісні. По формулі додавання шукана ймовірність Р(А) =Р(А
- несумісні. По формулі додавання шукана ймовірність Р(А) =Р(А  + А
+ А  ) =Р(А
) =Р(А  ) +Р(А
) +Р(А  ),
),
Р(А  ) =
) = 
 =
=  =
=  , Р(А
, Р(А  ) =
) =  =
=  =
= 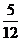 ,
,
Р(А) = Р(А) = 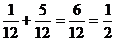
в) Нехай подія В - серед обраних виробів хоча б один бракований.
Можна вирішити це завдання за допомогою формули додавання, але рішення буде значно простіше, якщо перейти до протилежної події  - серед обраних виробів немає бракованих.
- серед обраних виробів немає бракованих.
 = А
= А  , Р(
, Р( ) = Р (А
) = Р (А  ) =
) =  , Р(В) = 1 - Р(
, Р(В) = 1 - Р( ) = 1 -
) = 1 -  =
= 
2. На двох автоматичних верстатах виготовляються однакові валики. Імовірність виготовлення валика вищого сорту на першому верстаті дорівнює 0,95, а на другому - 0,80. Виготовлені на обох верстатах не розсортовані валики перебувають на складі, серед них валиків, виготовлених на першому верстаті, у три рази більше, ніж на другому. Визначити ймовірність того, що навмання взятий валик виявиться вищого сорту.
Позначимо А - подію, що складається в тім, що взятий навмання валик виявиться вищого сорту;
B  - подія, що складається в тім, що взятий навмання валик
- подія, що складається в тім, що взятий навмання валик
зроблений на першому верстаті;
B  - подія, що складається в тім, що валик зроблений на другому
- подія, що складається в тім, що валик зроблений на другому
верстаті.
Застосувавши формулу повної ймовірності одержимо:
Р(А) = Р(В  )Р(А/ В
)Р(А/ В  ) + Р(В
) + Р(В  )Р(А/ В
)Р(А/ В  ).
).
Оскільки валиків, зроблених на першому верстаті, в 3 рази більше, ніж на другому, то Р(В  ) =
) = 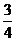 , Р(В
, Р(В  ) =
) =  .
.
У завданні дані умовні ймовірності: Р(А/ В  ) = 0,92,Р(А/ В
) = 0,92,Р(А/ В  ) = 0,80.
) = 0,80.
Шукана ймовірність: Р(А) = 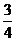
 = 0,89.
= 0,89.
3. В умовах Приклада 2, узятий навмання валик виявився вищого сорту. Визначити ймовірність того, що він зроблений на першому верстаті.
Використовуючи позначення Приклада 2, по формулі Баейса одержимо:
Р(В  /А) =
/А) =  =
=  = 0,76.
= 0,76.
4. Вироби деякого виробництва містять 5% браку. Знайти ймовірність того, що серед шести, узятих навмання виробів:
1) будуть два бракованих;
2) не буде бракованих;
3) буде хоча б один бракований.
Тут А – поява бракованого виробу, Р(А) = 0,05, Р(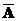 ) = 1- 0,05 = 0,95,
) = 1- 0,05 = 0,95,
n=6. По формулі Бернуллі
1) при m = 2, Р(6,2) = 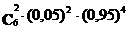 = 0,03;
= 0,03;
2) при m = 0, Р(6,0) = (0,95) 
 0,73;
0,73;
3) у цьому випадку завдання можна вирішити двома способами.
Перший спосіб. Використовуючи формулу додавання, одержимо
Р(6,1) + Р(6,2) = 
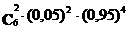
 0,27.
0,27.
Другий спосіб. Перейдемо до протилежної події - серед обраних виробів немає бракованих. Ймовірність цієї події обчислена в п.2) і дорівнює 0,73. Тоді шукана ймовірність
Р( 1 – 0,73 = 0,27.
1 – 0,73 = 0,27.
Варіанти завдань.
Таблиця 1. Варіанти до завдання 1.
| Пере- мінна | Номер варіанта | ||||||||||||||
| s | |||||||||||||||
| r | |||||||||||||||
| g | |||||||||||||||
| h | |||||||||||||||
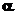 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| i | |||||||||||||||
| a | |||||||||||||||
| p | 1/3 | 1/5 | 1/4 | 1/6 | 1/8 | 1/9 | 1/3 | 1/5 | 1/4 | 1/6 | 1/8 | 1/9 | 1/9 | 1/8 | 1/6 |
| c |
Продовження таблиці 1.
| Пере- мінна | Номер варіанта | ||||||||||||||
| s | |||||||||||||||
| r | |||||||||||||||
| g | |||||||||||||||
| h | |||||||||||||||
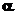 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| i | |||||||||||||||
| a | |||||||||||||||
| p | 1/6 | 1/8 | 1/3 | 1/9 | 1/9 | 1/3 | 1/4 | 1/8 | 1/8 | 1/8 | 1/3 | 1/6 | 1/9 | 1/9 | 1/3 |
| c |
 2018-01-08
2018-01-08 1824
1824







