Дифференциальное уравнение затухающих колебаний. Коэффициент затухания. Логарифмический коэффициент затухания

дифференциальное уравнение затухающих колебаний. Обозначим 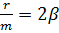,где -коэффициент затухания, 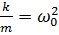,где -частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.

В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид: . Коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:

;

χ=βT.

Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда: , , χ=βT= .

Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , а то круговая частота обращается в нуль (), а (), колебания прекращаются. Такой процесс называется апериодическим.