Банк задач, тестирование официальное 2009 г. 4 страница

v_1min= √{2gR(1 + √2)} = √{4,83gR}.

Примечания.
а) Можно показать, что часть параболической траектории над точкой B не пересекает цилиндр.
б) Довольно легко определить также угол начального броска и расстояния AD. Расчеты дают

α ≥ 3π/8 = 67,5°, AD = R(1 + √2/2).

в) Обратите внимание на то, что точка F является фокусом параболы.
г) Минимальная скорость тела, если оно, перелетая цилиндр, все же касается в верхней точке траектории вершины может быть найдена из следующих соображений.
Воспользуемся законом сохранения энергии для точки E

mv₁²/2 = mv_x²/2 + mg2R.

Нормальное ускорение тела в верхней точке траектории

a_n= v_x²/R₁= gcosα₁,

где α₁ − угол между вектором скорости тела в точке траектории и горизонталью, радиус кривизны в данной точке. Для верхней точки

α₁= 0 и R₁= R, тогда v_x²= gR.

Сделаем подстановку в закон сохранения для верхней точки

v₁²= 5gR и v₁= √{5gR}.

Как видим v₁> v_1min.

Открытый сверху вагон, катящийся по рельсам без трения, заезжает на загрузку песка. Начальная скорость вагона v_o, масса пустого вагона m_o, масса загруженного песка m₁. Подача песка осуществляется равномерно так, что оно покрывает пол вагона слоем постоянной высоты. Найдите время загрузки Т вагона.
Примечание: форма вагона представляет собой параллелепипед.

Решение:
Введем одномерную систему координат Ox, совпадающей с рельсом (любым). Начало координат – передняя часть вагона перед началом засыпания песка; направление – вдоль скорости вагона. Координата x – положение передней стенки вагона (x_o= 0).

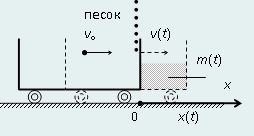
Координата x меняется со временем, когда весь вагон загрузится песком (через время T), она будет равна длине вагона: x(T) = L.
Так же, как видно из рисунка, такое положение начала координат позволяет заявить, что длина насыпанной части песка в момент времени t равна x(t).
Основа решения: закон сохранения импульса. Рассмотрим его проекцию на ось Ox (здесь не будем учитывать импульс падающего песка):

m_ov_o= const = m(t)v(t).

Так как масса с насыпанием песка увеличивается, то скорость вагона уменьшается.
Рассмотрим момент времени t (начало отсчета времени – начало засыпания песка). Найдем массу песка:

m_n= ρV = ρbhx, m_n(t) = ρbh × x(t),

где ρ – плотность песка, b – толщина вагона, h – высота слоя песка, x – координата.
Мы знаем, что

m_n(T) = m₁; x(t) = L; m₁= ρbhL,

отсюда

ρbh = (m₁/L),

и

m_n(t) = (m₁/L) × x(t).

Вернемся к закону сохранения импульса:

m_ov_o= m(t)v(t) = {(m₁/L)x(t) + m_o}v(t), m_ov_o= m(t)v(t) = {(m₁/L)x(t) + m_o}x^/(t). (1)

Получили дифференциальное уравнение, но решить его несложно, можно даже до конца его не решать. Перепишем (1) в другом виде:

m_ov_o= {(m₁/L)x(t) + m_o}dx/dt,

или

m_ov_o= {(m₁/L)x(t)dx/dt + m_odx/dt

и

m_ov_odt = {(m₁/L)x(t)dx + m_odx.

Проинтегрируем от начала отсчета времени (начало координат) до времени t (когда координата x):

₀∫^tm_ov_odt =₀∫^x(m₁/L)dx +₀∫^xm_odx,

 

m_ov_ot = (m₁/L)x²/2 + m_ox.

Получаем:

m_ox(t) +[m₁/(2L)]x²(t) = m_ov_ot.

В принципе, отсюда, решая квадратное уравнение можно получить функцию x(t), но нам для решения это не понадобиться. Зная, что x(T) = L, найдем T:

m_oL + m₁/(2L) × L²= m_ov_oT,

Откуда

T = (m_o+ m₁/2)L/(m_ov_o).

· Следующая задача

С поверхности бесконечной пластины с начальной скоростью v_o, направленной перпендикулярно пластине, вылетает электрон. Определите, на какое максимальное расстояние от пластины удалится электрон, если
а) над пластиной создано однородное электрическое поле, напряженности E, направленной перпендикулярно пластине;
б) над пластиной создано однородное магнитное поле, индукции B, направленной параллельно пластине;
в) над пластиной созданы однородное электрическое поле, напряженности E, направленной перпендикулярно пластине, и однородное магнитное поле, индукции B, направленной параллельно пластине.

Решение:
1) По мере удаления электрона от пластины возрастает его потенциальная энергия в электростатическом поле пластины.

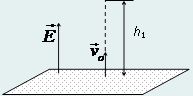
В точке максимального подъема кинетическая энергия (и скорость) обратится в нуль. По закону сохранения энергии

mv_o²/2 + 0 = 0 + eEh₁,

где m_o – масса электрона, e – его заряд.
Тогда

h₁= m_ov_o²/(2eE).

2) В магнитном поле на заряд будет действовать сила Лоренца, вследствие которой он будет двигаться по дуге окружности (пролетит пол-окружности и ударится о плоскость).

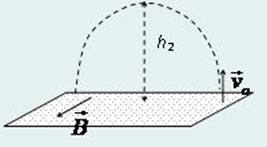
По второму закону Ньютона:

m_ov_o²/R = ev_oB

и

R = m_ov_o/(eB).

Из рисунка ясно, что максимальное расстояние от электрона до пластины – радиус окружности:

h₂= R = m_ov_o/(eB).

3) Рассмотрим электрон в некоторой точке A (рис.),

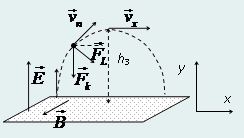
его скорость v_n. На него действуют силы:
F_k= Ee и F_L= e(v_n× B) (векторное произведение).
На ось Ox может иметь только проекцию только F_L.
Запишем второй закон Ньютона для этой проекции:
Ox: m_oa_x= F_Lcosα = ev_nBcosα,
но v_ncosα = v_nsin(90° − α) = v_ny – проекция скорости на ось Y.
Получаем: m_oa_x= eBv_ny, вспомним смысл ускорения и скорости:

m_odv_x/dt = eBdy/dt, m_odv_x= eBdy.

Взяв за начало координат точку запуска электрона, и с учетом того, что в начале движения v_x= 0, проинтегрируем:

₀∫^v_xm_odv_x=₀∫^yeBdy, m_ov_x= eBy. (1)

В процессе полета электрона, F_k и F_L только уменьшают его проекцию скорости на ось Oy (v_y) (F_k всегда направлена вниз, а F_L поворачивает ее, тем самым уменьшая проекцию). Можно утверждать, что в точке максимального удаления от пластины v_y= 0 (дальше будет становиться отрицательной и электрон начнет приближаться к пластине). Поэтому в точке максимального удаления v = v_x, и уравнение (1) для этой точки:

m_ov = eBh₃, v = eBh₃/m_o.

Закон сохранения энергии в момент вылета и в точке максимального подъема:

m_ov_o²/2 + 0 = m_ov²/2 + eEh₃,

m_ov_o²/2 = m_oe²B²h₃²/(2m_o²) + eEh₃,

выразим h₃:

h₃²× e²B²/(2m_o) + h₃eE − m_ov_o²/2 = 0,

h₃= [−m_oE ± m_o√{E²+ B²v_o²}]/(eB²),

h₃≥ 0, поэтому один корень отбрасываем:

h₃= (m_o/(eB²)) × (√{E²+ B²v_o²} − E).

· Следующая задача

На корабле, отплывающем от крутого берега, время от времени измеряют глубину моря. На расстоянии L₁= 100 м от берега глубина моря оказалась h₁= 150 м, на удалении L₂= 140 м зафиксирована глубина h₂= 200 м, на расстоянии L₃= 210 м от берега эхолот зарегистрировал два отражённых сигнала. Один из них соответствует глубине h₃= 300 м, а другой h₄= 400 м. Было высказано предположение, что второй сигнал обусловлен изменением знака наклона морского дна. Исходя из этого предположения, определите каков угол подъёма морского дна далее по курсу корабля.
При измерении глубины с корабля посылается направленная акустическая волна вертикально вниз. При взаимодействии со дном волна изотропно отражается во все стороны. На корабле регистрируется отражённый сигнал. При решении задачи могут понадобиться некоторые свойства эллипса. Напомним их. Сумма расстояний от любой точки эллипса до его фокусов − постоянная величина, равная длине его большей оси. Малая полуось эллипса b = √{a²− c²}, где a − большая полуось, а c − расстояние от фокусов эллипса до его центра. Уравнение эллипса имеет вид:

x²/a²+ y²/b²= 1,

где начало декартовой системы координат расположено в центре эллипса, ось x направлена вдоль большой оси, а y − вдоль малой. Нормаль к эллипсу в точке является биссектрисой угла между прямыми, соединяющими эту точку с фокусами эллипса.

· Следующая задача

Снег, лежащий на склоне гор, иногда приходит в движение, образуя снежные лавины. Снежные массы неожиданно начинают спускаться сверху, увлекая за собой всё, что находится на склоне горы. Энергия лавины быстро нарастает, превращая её в грозное стихийное бедствие. Для описания движения лавины воспользуемся следующей моделью.

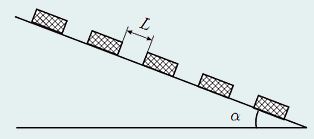
На длинной наклонной плоскости с углом α через одинаковые промежутки L расставлены тяжёлые бруски (рис.). От скольжения по плоскости их удерживают сила сцепления, которая исчезает при сколь угодно малом толчке. После освобождения бруски скользят с ничтожным трением. Если верхний брусок придёт в движение, он столкнётся со вторым бруском, далее цепочка из двух брусков столкнётся с третьим и так далее. Все соударения предполагаются абсолютно неупругими. В результате возникает длинная цепочка, к которой присоединяются всё новые и новые бруски. Этот процесс и моделирует движение лавины по горному склону.

1. Пусть в цепочке движется n брусков. Определите приращение кинетической энергии ΔE цепочки после столкновения с (n + 1)−м бруском по сравнению с энергией после столкновения с n-м бруском.

2. Найдите разность энергий цепочек из n>> 1 и k > n брусков E_k− E_n.

3. Как сказывается на движении лавины учёт силы трения? Ответьте на вопросы предыдущих заданий, полагая, что угол наклона плоскости α больше «лавиноопасного» угла β.

· Следующая задача

Одним из важных и обширных приложений классической механики является небесная механика, описывающая движение космических объектов.
В данной задаче речь идёт о движении двух планет Солнечной системы − Земли и Марса. Период обращения Земли вокруг Солнца равен T_E= 365 суток, а марсианский год составляет T_M= kT_E, где k = 1,88. В отдельные моменты времени планеты оказываются в положении, которое называют противостоянием. При противостоянии Марс виден с Земли в направлении, противоположном Солнцу. При этом он совершает так называемое «попятное движение», то есть вблизи точек противостояния меняет на противоположное направление своего движения относительно звёзд.
1. На рисунке показано положение Земли E, Марса M и Солнца S в противостоянии. Предполагая, что движение планет происходит по концентрическим окружностям вокруг Солнца, определите радиус R_М орбиты Марса, а также промежуток времени τ между двумя последовательными противостояниями, полагая известным радиус земной орбиты R_E= 1,50 × 10¹¹ м.

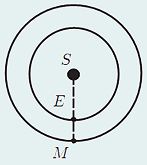
2. Считая, что планеты движутся по часовой стрелке (рис.), найдите, на какой угол φ повернётся линия противостояния за время τ.
3. Наблюдения показывают, что промежутки времени между последовательными противостояниями не одинаковы. Указанные промежутки плавно изменяются от значения τ_min= 764 суток до τ_max= 811 суток. Можно предположить, что это обусловлено отличием орбиты Марса от окружности. Считая, что движение Марса происходит по эллипсу, покажите, что промежуток времени между последовательными противостояниями вблизи перигелия (ближайшей к Солнцу точки орбиты) наибольший, а вблизи афелия (наиболее удалённой от Солнца точки орбиты) − наименьший. Найдите минимальное R_min и максимальное R_max удаление Марса от Солнца.

· Следующая задача

Для определения масс ионов используют масс-спектрографы. В школьном курсе физики вы познакомились с приборами, в которых пространственное разделение ионов различных масс происходит в постоянном магнитном поле. Возможны и другие физические принципы разделения ионов. Так, в динамических масс-спектрографах селекция ионов происходит благодаря различию скоростей движения ионов в электрическом поле.
Часть 1. Постоянное поле.
Предлагаем рассмотреть простейший динамический масс-спектрометр, схема которого изображена на рисунке.

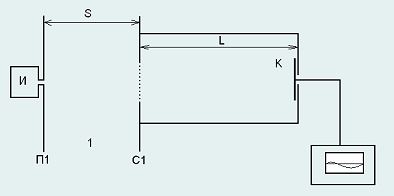
Однозарядные ионы вылетают из источника ионов И с пренебрежимо малой скоростью, затем попадают в область ускоряющего электрического поля 1, ширина которой равна S. В этой области электрическое поле создается постоянным напряжением U, приложенным к пластине П1, расположенной непосредственно у источника, и сетке С1. Ускорившиеся ионы, свободно пролетают через сетку, и, пройдя эквипотенциальный промежуток длиной L, попадают на коллектор (устройство, собирающее ионы), подключенный к прибору, регистрирующему силу ионного тока в зависимости от времени. Источник и регистрирующее устройство включают в момент времени t = 0. Источник является импульсным, то есть ионы испускаются в течение малого промежутка времени τ, плотность потока ионов в этом временном промежутке можно считать постоянной.
1.1 Пусть источник испускает одинаковые ионы массой m. Постройте график зависимости регистрируемого ионного тока от времени.
1.2 Пусть источник испускает ионы двух типов, массы которых отличаются незначительно и равны m и m + δm, причем δm << m. Присутствие ионов двух типов проявляется в виде двух импульсов на графике I(t). Ионы различных типов называются разрешёнными, если соответствующие им импульсы ионного тока не перекрываются во времени. Покажите, что минимальная разность масс ионов, которые разрешаются рассматриваемым прибором, удовлетворяет условию δm = α√m.
1.3 Получите формулу, связывающую коэффициент α с параметрами прибора. Рассчитайте численное значение этого коэффициента при τ = 1,0 × 10⁻⁶c, S = 0,30 м, L = 2,0 м, U = 200 B и для массы ионов, измеряемой в а.е.м. (атомных единицах массы).
1.4 Сможет ли масс-спектрометр с такими параметрами разрешить ионы ⁵⁴Fe⁺ и ⁵⁶Fe⁺
Заряд электрона e = 1,6 × 10⁻¹⁹Кл, постоянная Авогадро N_A= 6,02 × 10²³1/моль.

Часть 2. Высокочастотное поле.
Рассмотренный выше масс-спектрометр обладает рядом недостатков: во-первых, достаточно большие размеры, во-вторых, высокие требования к источнику ионов. Существуют более компактные масс-спектрометры, не требующие импульсных источников ионов.
Рассмотрим, так называемый, радиочастотный масс-спектрометр, схематически изображённый на рисунке.

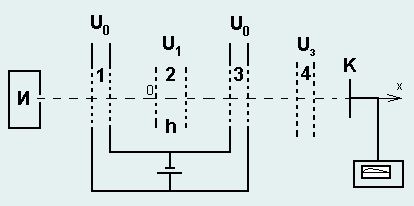
Источник однозарядных ионов работает непрерывно и скорость ионов на его выходе практически равна нулю. Поток ионов проходит через ряд сеток, между которыми создаются электрические поля различных типов. После их прохождения ионы собираются коллектором К, соединенным с измерителем ионного тока. К сеткам, ограничивающим промежуток 1, прикладывается постоянная разность потенциалов U_o= 1,0 кВ, создающая поле, ускоряющее ионы. Это же напряжение прикладывается к сеткам, ограничивающим промежуток 3, в котором оно создает постоянное тормозящее электрическое поле. В промежутке 2, ширина которого h, создается высокочастотное электрическое поле. К границам этого промежутка прикладывается переменное напряжение, циклическая частота которого ω может изменяться в пределах (5 ÷ 15) × 10⁶c⁻¹. Амплитудное значение этого напряжения равно U₁= 1,0 B. Наконец, к промежутку 4 прикладывается регулируемая задерживающая разность потенциалов U_з, величина которой близка к амплитудному значению напряжения высокочастотного поля.
Прибор регистрирует значение ионного тока, усредненное по промежутку времени, значительно превышающему период изменения высокочастотного поля.
Ионы, ускорившиеся в промежутке 1, попадают в область высокочастотного поля в различные моменты времени. Изменение энергии ионов в области высокочастотного поля зависит от типа ионов и момента попадания в рассматриваемую область. При некоторых условиях приращение энергии этих ионов может быть достаточным для того, чтобы преодолеть области задерживающих полей 3 и 4. Эти ионы попадут на коллектор и создадут регистрируемый ионный ток. Зависимость среднего ионного тока от частоты переменного поля в промежутке 2 может иметь ряд достаточно резких максимумов, положение которых зависит от масс исследуемых ионов. Тем самым существует возможность различать ионы различных типов. В данной части вам предлагается проанализировать работу этого прибора.

2.1 Определите скорость v₁ иона массы m после прохождения ускоряющего напряжения в промежутке 1 и максимальное ускорение a₁ этого иона в промежутке 2. Найдите численное значение v₁ для иона ⁵⁶Fe⁺.
2.2 Оцените по порядку величины ширину промежутка 2, при которой указанный ион, влетев в промежуток в удачный момент времени, максимально увеличит свою энергию в высокочастотном поле при его частоте ω = 10 × 10²c⁻¹.
Совместим начало отсчета оси координат Ox с началом области высокочастотного поля.
2.3 Пусть ион массы m, прошедший ускоряющий промежуток 1, попадает на левую сетку промежутка 2 в момент времени τ, при котором разность потенциалов в промежутке 2 U = U₁sinωτ. Найдите зависимость ускорения, скорости и координаты иона от времени a(t), v(t), x(t), где t отсчитывается от момента попадания иона в промежуток 2.
2.4 Из-за малости U₁, изменение скорости иона в промежутке 2 незначительно, поэтому, при расчете времени пролета этого промежутка, изменением скорости иона можно пренебречь.
Определите время t₁ пролёта этого промежутка для иона массы m, используя это приближение. Оцените относительную погрешность полученного выражения.
2.5 При заданной ширине промежутка высокочастотного поля h, изменение энергии ΔE ионов массы m, при его пролёте, зависит от частоты переменного поля ω и момента времени прихода τ. Установите зависимость изменения энергии иона в этой области от указанных величин ΔE(ω, τ).
Воспользуйтесь формулой:

cosα − cosβ = −2sin[(α + β)/2]sin[(α − β)/2].

2.6 Так как источник ионов работает непрерывно, то ионы попадают в область высокочастотного поля в произвольные моменты времени τ. Некоторые из них, попадающие в эту область в оптимальные моменты времени (которые, возможно зависят от частоты поля), приобретают максимальную энергию (при заданном значении частоты поля ω) ΔE(ω). Для анализа зависимости изменения энергии от параметров установки и типа ионов удобно представить зависимость ΔE_max от безразмерного параметра φ = ωh/v_o − изменение фазы высокочастотного поля за время пролета иона. Постройте примерный график зависимости ΔE_max от указанного параметра.
Полученная вами функция, скорее всего, имеет множество экстремумов в зависимости от φ, многие из которых пригодны для анализа состава потока ионов. Если частота переменного поля такова, что ионы определенной массы m, приобретают дополнительную энергию большую, чем ионы других близких масс, то, изменяя задерживающее напряжение, существует возможность выделить из всего потока ионов только ионы данной массы m. В этом случае только эти ионы будут создавать ионный ток. Ионы другой массы будут достигать коллектора при другой частоте переменного поля. Таким образом, в зависимости ионного тока от частоты поля будут наблюдаться максимумы, каждый из которых соответствует ионам определенной массы.
2.7 Укажите на графике значение параметра φ_o, вблизи которого рассматриваемый прибор способен анализировать состав ионного потока наиболее эффективно.
Пусть источник испускает одинаковые ионы массы m. Ширина промежутка h.
2.8 Определите частоту поля ω_o, при которой приращение энергии этих ионов будет максимально в указанной оптимальной области работы прибора. Найдите это максимальное приращение энергии ΔE_max и значение времени прихода ионов τ_o, при котором оно реализуется.
2.9 Пусть частота поля равна найденной частоте ω_o. Чему должно быть равно максимальное значение запирающего напряжения U_з0, при котором ионный ток становится равным нулю. Представьте это значение в виде U_з0= αU₁, рассчитайте численное значение коэффициента α с точностью до трех значащих цифр.
2.10 Для регистрации тока запирающее напряжение нужно немного уменьшить. Пусть U_з= U_з0(1 − η), где η > > 1. Найдите зависимость ионного тока от величины η. Сила тока, создаваемая рассматриваемыми ионами массы m, на выходе источника равна I_o.
2.11 При заданной величине η можно регистрировать ток даже в том случае, если частота ω отличается от ω_o на некоторую малую величину Δω. Найдите максимальное значение этой величины.
2.12 Пусть источник испускает ионы двух близких масс m и m + δm. При заданном η определите при каком минимальном отношении δm/m эти ионы ещё могут быть разрешены.

· Следующая задача

В данной задаче рассматривается достаточно простая модель, демонстрирующая принципы работы оптического квантового генератора.
Согласно квантовой теории атомы и молекулы могут находиться в дискретном наборе состояний, энергии которых имеют строго определенные значения. Невозбужденные молекулы находятся в основном состоянии с минимально возможным значением энергии. При поглощении кванта света, энергия которого равна разности энергий возбужденного и основного состояний, молекула переходит в возбужденное состояние. Поглощательная способность молекулы характеризуется так называемым сечением поглощения σ.

Часть 1. Поглощение и испускание.
1.1 Пусть световой поток малой плотности I_o (число фотонов пересекающих площадку единичной площади в единицу времени) падает на тонкий слой вещества толщиной Δx, концентрация поглощающих молекул в котором равна γ, причем среднее расстояние между молекулами значительно превышает их размеры.

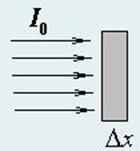
Определите плотность светового потока I на выходе из этого слоя. Относительное изменение плотности потока p = I/I_o при прохождении поглощающего слоя назовем коэффициентом пропускания.
Поглощающие молекулы можно представить в виде шариков с площадью поперечного сечения равной сечению поглощения σ.