Банк задач, тестирование официальное 2009 г. 3 страница

x₁= x_o

 

α₁= −(n − 1) × (1/R₁+ 1/R₂) × x_o+ α_o.

4. Используя результаты п. 3, получите формулу для фокусного расстояния F тонкой линзы.
5. Получите «формулу тонкой линзы», связывающую расстояние от предмета до линзы a с расстоянием от линзы до изображения b:

1/a + 1/b = 1/F.

6. Рассмотрите оптическую систему состоящую из двух сферических зеркал, повернутых навстречу друг другу (рис. 3). Обозначим радиусы кривизны одного зеркала R₁ (его центр точка O₁); другого – R₂ (центр – O₂); расстояния между зеркалами – d. Цель исследования – выяснить при каких параметрах системы произвольный световой луч AB не будет покидать данную оптическую систему.

Рассматриваемая нами система является оптическим резонатором, повсеместно используемым в оптических квантовых генераторах (лазерах). Если для него выполняется условие задачи, то такой резонатор называется устойчивым, в противном случае неустойчивым.
Заменим систему зеркал на бесконечную цепочку линз (рис. 4), фокусные расстояния которых равны фокусным расстояниям зеркал, которые, в свою очередь, известны:

F₁= R₁/2; F₂= R₂/2.

Понятно, что такая система полностью эквивалентна резонатору.

6.1. Используя линейные преобразования, полученные ранее, запишите формулы преобразований для произвольного луча за полный проход резонатора. Выразите формулы этих преобразований через безразмерные параметры, определяющие геометрию оптической системы

ξ₁= 1 − d/R₁; ξ₂= 1 − d/R₂.

6.2. В некоторых случаях явные выражения для параметров луча могут быть представлены в виде x_n= A × γⁿ; y_n= B × γⁿ, где γ – некоторая постоянная. Выразите возможные значения этого параметра параметры системы ξ₁, ξ₂.
При каком соотношении между параметрами ξ₁, ξ₂, резонатор будет устойчивым? Изобразите область устойчивости на диаграмме (ξ₁, ξ₂).

· Следующая задача

«Объясняя» возникновение радуги, авторы учебных пособий весьма часто ограничиваются указанием на то, что это замечательное природное явление демонстрирует явление дисперсии света. Иногда приводят типичный рисунок двойного преломления луча света в сферической капле воды (рис. 1), позаимствованный еще из работы Р.Декарта. Приведенные утверждения справедливы: действительно изображение радуги формируют солнечные лучи, дважды преломившиеся на поверхности капли (и конечно, один раз отразившиеся от ее внутренней поверхности); действительно показатель преломления воды зависит от длины волны падающего света, поэтому углы выхода лучей из капли различны для различных длин волн. Однако объяснение и описание радуги не столь просто, как это кажется на первый взгляд, хотя эффекты данного явления вполне объяснимы в рамках геометрической оптики.

Рассмотрим прохождение лучей через сферическую каплю.

Назовем оптической осью прямую O₁O₂, проходящую через центр капли и параллельную падающему лучу S_o. Обозначим:
S₁ – луч, сразу отразившийся от поверхности капли;
S₂ – луч, испытавший два преломления на поверхности капли;
S₃ – луч, испытавший два преломления и одно отражение внутри капли;
S₄– луч, испытавший два преломления и два отражение внутри капли.
Углы, под которыми лучи отходят от капли θ₁, θ₂, θ₃, θ₄, будем отсчитывать от оптической оси. Назовем прицельным параметром ρ отношение расстояния между падающим лучом и оптической осью к радиусу капли. (Для лучей, падающих на каплю, этот параметр изменяется от −1 до +1).
1. Найдите зависимости углов, под которыми лучи отходят от капли θ₁, θ₂, θ₃, θ₄, от прицельного параметра ρ.
2. Покажите, что зависимости углов θ₁, θ₂ от прицельного параметра ρ являются монотонными. Покажите, что для лучей S₃, S₄ существуют минимальные значения углов отклонения θ₃, θ₄. Найдите значения этих минимальных углов.
3. Покажите, что лучи, вышедшие из различных капель под одинаковыми углами к оптической оси, расположенных в разных точках пространства, дают изображение на сетчатке глаза в виде дуги окружности. Постройте ход этих лучей в глазу человека.
4. Покажите, что минимальным углам отклонения соответствует яркая граница, которая определяет угловой размер радуги.
5. Вычислите угловой наблюдаемый размер α основной и вторичной радуги. (На рис. 3 показана только одна из них).

6. Вычислите угловую ширину δα каждой дуги радуги.
Значения показателя преломления воды, для различных длин волн.
Длина волны (нм), цвет: 759,0 (красный); 589,8 (желтый); 486 (голубой); 397,0 (фиолетовый)
Показатель преломления: 1,329; 1,333; 1,337; 1,344

· Следующая задача

В интерференционной схеме Юнга две узкие параллельные щели S₁ и S₁, расстояние между которыми равно a, освещаются плоской волной, падающей нормально на экран со щелями. На расстоянии L (L >> a) расположен экран, на котором наблюдается интерференционная картина. Исследуется зависимость интенсивности света на этом экране от координаты x (x << L) − расстояния до оси симметрии системы.

1. Щели освещены монохроматической волной с длиной волны λ. Найдите распределение интенсивности света на экране. Определите ширину интерференционной полосы (расстояние между двумя последовательными максимумами интенсивности).
2. Пусть щели освещены двумя монохроматическими волнами равной интенсивности с близкими длинами волн λ и λ + Δλ (Δλ >> λ). Опишите распределение интенсивности света на экране в этом случае.
3. Щели осветили немонохроматическим излучением, содержащим непрерывный спектр длин волн, лежащих в узком интервале от λ_o и λ_o+ Δλ (Δλ >> λ_o). Опишите распределение интенсивности света на экране в этом случае.
4. Рассмотрим следующую модель частично когерентного света. Световой поток представим в виде случайной совокупности цугов − ограниченных во времени и пространстве участков синусоидальных волн. Все цуги имеют одинаковую частоту, амплитуду и длительность τ. Однако начальные фазы колебаний изменяются от цуга к цугу случайным образом.

Опишите интерференционную картину на экране в интерференционной схеме Юнга, если щели освещены частично когерентным светом, модель которого представлена выше. Покажите, что качественно интерференционная картина совпадает с картиной, описанной в п.3. Установите связь между величинами τ и Δλ (а также с шириной спектра Δv), чтобы две описанные интерференционные картины качественно совпадали.

· Следующая задача

Все взаимодействия, все сигналы распространяются с конечной скоростью, поэтому любая воспринимаемая нашими органами чувств и приборами информация «запаздывает»: то, что мы видим «сейчас», на самом деле произошло «раньше». Нам повезло − скорость света настолько велика, что упомянутое «запаздывание» практически не оказывает никакого влияния на наше поведение. Тем, не менее, в некоторых случаях его необходимо учитывать. Этой проблеме и посвящена данная задача.

Положение некоторого движущегося тела A (объекта наблюдения) с помощью сонара (звукового радара) S. Сонар посылает очень короткий звуковой сигнал в виде изотропной сферической волны и улавливает отраженную от тела волну. Скорость распространения волны известна и равна c.
Сонар фиксирует следующие величины:
время, когда послан сигнал − t_o; время прихода отраженной волны − τ, направление на точку, из которой пришел отраженный сигнал, задаваемое с помощью угла φ.
Будем считать, сигналы сонара каким-то образом различаются, поэтому компьютер сонара в момент регистрации отраженного сигнала, точно «знает», когда именно этот сигнал был послан. Затуханием сигнала можно пренебречь.
Введем систему координат xOy, начало которой совместим с сонаром. Будем рассматривать тела, движущиеся в этой плоскости.

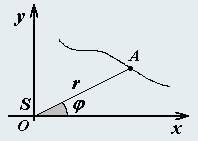
Для определения положения тела приняты следующие правила: положение тела в момент прихода отраженного сигнала задается измеренным углом φ, а расстояние до него рассчитывается по формуле

r^/= (τ − t_o)c/2. (1)

Определенное по этим правилам положение тела будем называть изображением объекта.
1. Пусть наблюдаемое тело движется равномерно вдоль оси OX. Закон движения тела имеет вид

x = x_o+ v_ot. (2)

1.1. Определите скорость движения изображения тела.
1.2. Найдите закон движения изображения.
2. Наблюдаемое тело движется равноускоренно вдоль оси OX. Закон движения тела имеет вид

x = at²/2. (3)

2.1. Определите скорость и ускорение движения изображения тела, как функции времени. Постройте примерные графики этих зависимостей.
2.2. Найдите закон движения изображения.
3. Наблюдаемое тело движется в плоскости xOy по закону известному закону

x = x(t), y = y(t). (4)

3.1. Получите общее уравнение, связывающее время отправления сигнала t_o и время прихода отраженного сигнала τ.
3.2. Покажите, что траектория движения изображения совпадает с траекторией движения тела.
3.3. Считая, что скорость сигнала значительно превышает скорость движения наблюдаемого тела и время распространения сигнала также является малой величиной, получите приближенные явные выражения для определения координат изображения, учитывающие малые поправки, связанные с запаздыванием, только первого порядка по малому параметру γ = v/c.
4. Пусть наблюдаемое тело движется по закону

x = v_ot, y =l. (5)

4.1. Найдите зависимость скорости движения изображения тела от времени. Постройте примерный график этой зависимости.
4.2. Найдите зависимость скорости движения изображения тела от его наблюдаемой координаты x^/. Постройте примерный график этой зависимости.
5. Предложите правила определения закона движения тела, дающие точный результат при определении закона движения наблюдаемого объекта.

· Следующая задача

Движение со сверхзвуковой скоростью − давняя мечта авиаконструкторов. Однако при таких скоростях возникает ряд неожиданных эффектов, исследовать которые − ваша задача.
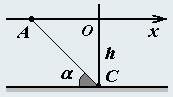
1. Самолет движется горизонтально на высоте h над поверхностью земли (Землю считайте плоской) с постоянной скоростью V. Наблюдатель находится в точке C на поверхности земли.

Совместим ось Ox с траекторией движения самолета, ось Oy направим вертикально, проходящую через точку наблюдателя. Закон движения самолета запишем в виде

x = Vt. (1)

Скорость звука в воздухе известна и равна c.
1.1. В какой момент времени τ звуковая волна, испущенная самолетом в точке с координатой x, достигнет наблюдателя?
1.2. Постройте примерные графики зависимости времени прихода волны от координаты точки ее испускания τ(x) для значений следующих скорости самолета:

V₁= 0,10c; V₂= 0,50c; V₃= c; V₄= 1,5c; V₅= 2,0c.

Считайте, что t ∈ [− ∞, +∞].

2. «Гудящий» самолет начинает двигаться из начала координат в момент времени t = 0. Временем разгона самолета можно пренебречь.
2.1. Определите область пространства (множество точек (x, y)), до которой дошла звуковая волна к моменту времени t. Для аналитического описания этой области можете выбрать ту форму, которая вам нравится.

2.2. Постройте эту область для следующих значений скорости движения самолета:

V₁= 0,50c; V₃= c; V₅= 2,0c.

 

3. В качестве характеристики звуковой волны примем отклонение давления воздуха Δp от среднего давления. Будем также считать, что неподвижный самолет испускает сферическую монохроматическую волну с частотой ν _o. Пусть самолет движется так, как описано в пункте 1. Считайте, что амплитуда звуковой волны убывает обратно пропорционально расстоянию до источника.
3.1. Запишите выражение для величины Δp в точке наблюдения, как функцию времени.

3.2. Постройте примерный график зависимости частоты звука, воспринимаемого наблюдателем, от времени. Предварительно дайте ваше определение «частоты в данный момент времени». Рассмотрите следующие значения скорости движения самолета:

V₁= 0,50c; V₃= c; V₅= 2,0c.

3.3. Пусть звук самолета пришел из точки A, направление на которую задается углом α над горизонтом. Найдите зависимость частоты пришедшего звука от этого угла.
4. Узкий пучок электронов движется в воде со скоростью V = 0,90c, где с − скорость звука в вакууме. Торможением электронов можно пренебречь.

Показатель преломления воды n = 1,33. При движении электронов возникает свечение Вавилова − Черенкова. На оси пучка и перпендикулярно ему расположена собирающая линза радиуса r = 5,0 см с фокусным расстоянием F = 50 см, на расстоянии a = 45 см за ней плоский экран.
Укажите область экрана, освещенную, благодаря излучению электронов.

· Следующая задача

Водопроводный смеситель холодной (T₁= 10 °C) и горячей (T₂= 70 °C) воды состоит из двух одинаковых труб AB и CB, переходящих в удлинитель BD (рис.). Краны K₁ и K₂ регулируют расход q (т.е. объем воды, проходящий через трубу в единицу времени) и температуру T воды, выходящей из смесителя.
Опыт показывает, что расход воды через трубу AB (или CB) пропорционален разности гидростатических давлений p_A и p_B на ее концах q = αC(p_A− p_B), где α − некоторый безразмерный коэффициент «открытия крана», принимающий значение от нуля (кран закрыт) до единицы (кран полностью открыт), а C − некоторый постоянный размерный коэффициент для данной трубы.

Расход воды через удлинитель BD также пропорционален разности давлений жидкости на его концах q = C(p_B− p₀), где p₀ − нормальное атмосферное давление на выходе из трубы в точке D (см. рис.).
Давления в магистралях холодной p₁= p_A= 3,0 атм. и горячей p₂= p_В= 2,6 атм. труб поддерживаются постоянными. Воду будем считать несжимаемой жидкостью, а потери теплоты при прохождении смесителя − пренебрежимо малыми.
Если полностью открыть (α₁= 1,0) кран холодной воды при полностью закрытом кране горячей воды, то расход воды будет равен q₁= 1,4 л/с.

1. Вычислите значение коэффициента C и укажите его размерность.

2. Найдите расход q₂ воды при полном открытии крана с горячей водой (при закрытом втором кране).

3. Вычислите расход воды q₃ и ее температуру T₃ в случае, когда два крана открыть полностью (α₁= α₂= 1,0).

4. Найдите расход воды q₄ и ее температуру T₄ в случае, когда один кран холодной воды открыт на α₁= 0,30, а кран горячей − на α₂= 0,70.

5. В «час пик» при большом количестве пользователей давление p₂ в магистрали горячей воды может значительно упасть. При каком давлении p_2min подача горячей воды в смеситель полностью прекратится, если кран холодной воды открыт на α₁= 0,30, а кран горячей − на α₂= 0,70?

· Следующая задача

Часто простейшие модели позволяют достаточно эффективно описывать сложные механические системы. Например, при прыжке человек приседает, слегка нагнувшись, затем толкается ногами, распрямляет корпус и, собственно, … взлетает! Попробуем описать этот процесс с помощью «гантельной» модели человека с нежесткой связью.
Представим человека в виде упрощенной механической модели, состоящей из двух одинаковых грузов некоторой массы, расстояние между которыми может регулироваться человеком сознательно по требуемому закону (Рис. 1).

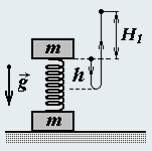
В рамках этой модели прыжок человека вверх описывается следующим образом: верхний груз опускают на расстояние h = 30 см (человек приседает). Затем «включаются» «мышцы ног», развивающие постоянную вертикальную силу F = η × mg, где η − некоторый постоянный безразмерный «коэффициент перегрузки», действующую между грузами. По достижении верхним грузом исходного положения работа мышц прекращается, и расстояние между грузами при дальнейшем движении остается неизменным. Для расчета примите, что η = 7,0.

1. Вычислите максимальную высоту H₁, на которую поднимется нижний груз при подобном прыжке. Чему равно время t₁ отталкивания от плоскости? Вычислите КПД К прыжка в рамках данной модели.
2. Предположим, что человек помещен на массивную горизонтальную платформу, совершающую гармонические колебания с амплитудой A = 20 см и частотой ν = 1,0 Гц (Рис. 2).

Человек может подпрыгнуть в произвольной точке траектории, причем можно считать, что параметры прыжка будут аналогичны параметрам в пункте 2.1 задачи. На какую максимальную высоту H₂ может подпрыгнуть человек с массивной платформы?
3. В рамках данной модели рассмотрим раскачивание человека на качелях длиной L методом «сел-встал» (рис. 3).

Суть метода проста: в одних нужных точках траектории нужно вставать, а в других − садится, причем в процессе движения человек от качелей не отрывается. Будем считать, что при вставании человека масса m приближается к оси вращения на расстояние h = 0,10L (h << L), а при приседании она возвращается обратно. Предположим качели отклонили на угол α_o= 10° и отпустили. На какой максимальный угол α могут отклониться качели за один период колебаний?
4. При тренировке космонавты крутят «солнышко», делая полный оборот в вертикальной плоскости на качелях длиной L. В нижней точке траектории угловая скорость вращения космонавта ω_o. Методом «сел-встал», описанным в предыдущем пункте задачи, космонавт может изменить угловую скорость ω вращения качелей за один оборот. Причем это нужно делать циклически, возвращаясь в исходное положение в нижней точке траектории. На какую величину Δω космонавт может увеличить угловую скорость вращения в нижней точке траектории методом «сел-встал» за один оборот качелей? Время вставания и приседания считайте достаточно малым.

Примечание: при вращательном движении в отсутствие моментов внешних сил справедлив закон сохранения момента импульса: произведение импульса p материальной точки на расстояние до оси вращения r есть величина постоянная

m₁v₁r₁= m₂v₂r₂⇔ m₁ω₁r₁²= m₂ω₂r₂².

Многие свойства кристаллов могут быть объяснены на основе законов классической физики. В данном задании вам необходимо оценить некоторые характеристики ионного кристалла, в качестве которого рассматривается кристалл поваренной соли NaCl.

Кристаллическая решетка поваренной соли является простой кубической, то есть ионы разных знаков (положительные Na⁺(относительная атомная масса A_rNa= 23) и отрицательные Cl⁻ (A_rCl= 35)) расположены в узлах кубической решетки. Радиусы этих ионов приблизительно равны.
В данном задании эти ионы следует рассматривать как жесткие равномерно заряженные непроводящие сферы одинаковых радиусов. При расстояниях между ионами большими или равными диаметру иона взаимодействие между ними является чисто электростатическим

Часть 1. «Ионные радиусы»
Плотность поваренной соли равна ρ = 2,16 × 10³кг/м³. Определите средний ионный радиус рассматриваемых элементов.
Часть 2. «Растворимость»
2.1. Рассчитайте энергию взаимодействия одного иона кристалла со всеми остальными.
2.2. Кристаллы поваренной соли могут растворяться в различных жидкостях, полностью распадаясь на отдельные ионы. Оцените, какова должна быть минимальная диэлектрическая проницаемость жидкости ε_min, чтобы соль могла растворяться в ней.
2.3. Диэлектрическая проницаемость воды равна ε = 81. Рассчитайте удельную теплоту растворения (количество теплоты, выделяющейся при растворении единицы массы) поваренной соли в воде.
Заряд электрона e = 1,6 × 10⁻¹⁹Кл, постоянная Авогадро N_A= 6,02 × 10²³моль⁻¹.
Диэлектрическая постоянная ε_o= 8,85 × 10⁻¹²Ф/м.
При решении задачи Вам может пригодиться следующая сумма:

Если же Вы столкнетесь с ещё какой-либо трудно вычисляемой суммой, обозначьте ее буквой, которая Вам нравится.

· Следующая задача

На горизонтальной плоскости находится цилиндрическая труба, радиусом R. Какую минимальную скорость необходимо сообщить телу, находящемуся на горизонтальной плоскости, чтобы перебросить его через цилиндрическую трубу?

Решение:
Траектория тела − это парабола, которая касается цилиндра в симметрично расположенных точках B и B^/ на двух сторонах ствола (рис.).

Тело удаляется от точки бросания с начальной скоростью v₁ под углом α к горизонту. В точках касания B и B^/ скорость тела v₂составляет угол β с горизонталью.
Выберем угол β в качестве независимой переменной задачи. Тогда в точке B вертикальная составляющая скорости равна

v₂sinβ = gt₂,

где t₂ − время полета на участке BC траектории (C − максимальная точка подъема, максимум параболы). Соответствующее горизонтальное перемещение BF равно

v₂t₂cosβ = Rsinβ.

После перемножения этих двух уравнений получаем

v₂²= gR/cosβ.

Закон сохранения энергии при полете между точками A и B дает

mv₁²/2 = mv₂²/2 + mg(R + Rcosβ),

или

v₁²= v₂²+ 2gR(1 + cosβ) = gR/cosβ + 2gR(1 + cosβ).

Мы получили выражение для начальной скорости в виде

v₁²= 2gR(1 + cosβ + 1/(2cosβ))

и можем вычислить минимальное значение v₁, используя дифференциальное исчисление. Приравняв производную

d(1 + cosβ + 1/(2cosβ))/dβ.

к нулю, получаем cos²β = 1/2. Таким образом, минимальный угол, который дает минимум начальной скорости, равен 45°.
Имеется и другой метод, который использует неравенство между средним арифметическим и средним геометрическим. В нашем случае можно записать

(1/2)(cosβ + 1/(2cosβ)) ≥ √{cosβ/(2cosβ)} = √2/2,

так что минимальное значение суммы cosβ + 1/(2cosβ) равно √2, откуда следует, что β = 45°.
Это и есть угол, под которым тело касается цилиндра при полете в оптимальном случае. Если допустить β = 0 (точка E), то потребуется большая начальная скорость, так как cosβ + 1/(2cosβ) = 1,5 > √2. Из этого следует, что траектория с минимальной начальной скоростью не касается ствола в его самой высокой точке (точка E). Гравитационная потенциальная энергия тела больше на пике параболы, чем в высшей точке цилиндра, но его кинетическая энергия и полная энергия меньше, чем они были бы для траектории, касающейся вершины.
Таким образом, минимальная начальная скорость тела равна