Банк задач, тестирование официальное 2009 г. 2 страница

2. При каком соотношении между параметрами μ и ξ шайба столкнется со стержнем только один раз? Изобразите схематически эту область параметров на диаграмме (μ, ξ).

3. При каком соотношении между параметрами μ и ξ после второго удара шайба будет двигаться с прежней скоростью v_o?

4. Пусть ξ = 0,333, μ = 0,330. На какой угол изменится направление вектора скорости шайбы после всех ее столкновений со стержнем?

Исследуется движение без трения небольшой шайбы (которую можно считать материальной точкой) по внутренней поверхности конуса, ось которого Z вертикальна, а тангенс угла полураствора α равен k.

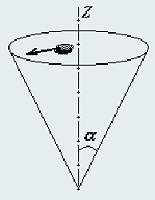
1. Какова должна быть скорость шайбы v_o, чтобы она могла двигаться по поверхности конуса в горизонтальной плоскости на высоте z_o от вершины конуса?

2. Шайбе, находящейся на высоте z_o от вершины конуса, сообщили скорость v в горизонтальном направлении вдоль поверхности конуса. Найдите пределы изменения координаты z шайбы в процессе ее движения.

3. Шайба движется в горизонтальной плоскости на высоте z_o от вершины конуса. Затем в результате толчка ее скорость увеличивается на небольшую величину v (направление вектора скорости при этом не изменяется). Найдите в каких пределах будет изменяться координата z шайбы в процессе движения и период ее колебаний вдоль вертикальной оси.

4. Шайба движется в горизонтальной плоскости на высоте z_o от вершины конуса. Затем ей толчком сообщают небольшое приращение скорости v, направленное вверх вдоль образующей конуса v < < √(gz_o). Найдите в каких пределах будет изменяться координата z шайбы в процессе движения и период ее колебаний вдоль вертикальной оси.

Рекомендуем воспользоваться приближенной формулой (1 + x)⁻²≈ 1 − 2x + 3x².

· Следующая задача

Оборотный маятник представляет собой тонкий однородный стержень длиной l, по которому можно перемещать две одинаковых массивных чечевицы A₁ и A₂. Положение чечевиц определяется координатами x₁ и x₂. Маятник может колебаться в вертикальной плоскости, будучи подвешенным на упорах S₁ или S₂ (в этом случае его необходимо перевернуть). Масса стержня значительно меньше массы чечевиц. Чечевицы можно считать материальными точками. Расстояния от упоров до концов стержня одинаковы и равны α.

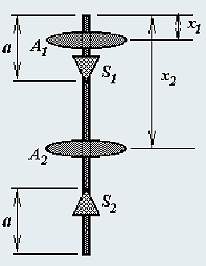
1. Найдите периоды колебаний маятника в прямом (на упоре S₁) и обратном (на упоре S₂) положениях в зависимости от x₁ и x₂.

2. Постройте график зависимости периода колебаний маятника в прямом положении при x₁= a/2 от положения второй чечевицы.

3. Найдите множество значений x₁, x₂, при которых период колебаний маятника T₁ в прямом положении один и тот же. Постройте эти множества точек на диаграмме (x₁, x₂) для различных значений T₁. Постройте аналогичные кривые для колебаний маятника в обратном положении.

4. На диаграмме (x₁, x₂) постройте множество значений (x₁, x₂), при которых периоды колебаний маятника в прямом и обратном положениях равны и постоянны. Покажите, что этот период равен периоду колебаний математического маятника с длиной равной расстоянию между упорами.

Бесконечная цепочка состоит из одинаковых шариков (масса каждого m), соединенных одинаковыми легкими пружинами (жесткость каждой γ). В положении равновесия расстояния между шариками равны l, пружины немного растянуты так, что сила натяжения каждой равна T_o.

 

Часть 1. Продольные волны.

Допустим, что каждый шарик может двигаться только в направлении вдоль цепочки.

1. Найдите собственную частоту колебаний одного из шариков ω_o, если два соседних закреплены.

2. По цепочке распространяется продольная волна. Найдите сдвиг фаз между колебаниями двух соседних шариков при частоте волн w.

3. При каких частотах колебаний ω по цепочке могут распространяться бегущие волны?

4. Найдите скорость распространения продольной волны по цепочке. Постройте примерный график этой зависимости.

5. Найдите скорость распространения продольной волны при частотах ω << ω_o. Покажите, что полученное выражение можно считать аналогом формулы для скорости звука в упругой среде с = √(E/ρ), где E − модуль Юнга, ρ − плотность среды.

6. В цепочке неподвижно закрепили неподвижно два шарика так, что между ними оказалось n шариков. Определите все частоты собственных колебаний этого участка цепочки, соответствующие различным модам стоячих волн.

Часть 2. Поперечные волны.

Пусть шарики способны перемещаться только в направлении перпендикулярном цепочке, причем их смещения малы (Δx << l).

1. Определите частоту поперечных колебаний одного шарика, если два соседних закреплены.

2. Найдите скорость распространения поперечной волны по цепочке.

3. Найдите скорость распространения поперечной волны при частотах ω << ω_o. Покажите, что полученное выражение можно считать аналогом формулы для скорости поперечных волн в упругой среде с = √(G/ρ), где G − модуль сдвига, ρ − плотность среды.

4. Найдите минимально возможную длину волны, которая может распространяться по цепочке.

5. На основании качественных рассуждений определите, как зависит скорость распространения поперечной волны от ее амплитуды, когда смещение шариков сравнимо с расстоянием между ними.

Один моль идеального одноатомного газа совершает циклический процесс, изображенный на рисунке: 1 → 2 прямая, 2 → 1 − адиабата.

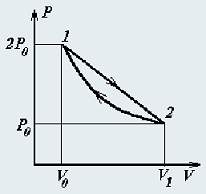
1. Найдите отношение V₁/V_o.

2. Какова максимальная температура газа в цикле?

3. Постройте примерный график зависимости теплоемкости газа на участке 1 → 2 от его объема.

4. Постройте график зависимости количества теплоты, полученной газом при расширении на участке 1 → 2, от его объема.

5. Найдите КПД цикла.

Рассмотрите свойства идеального кристалла с кубической решеткой, образованного одинаковыми атомами массой m. Потенциальная энергия взаимодействия двух атомов в кристалле зависит от расстояния между их центрами r по закону

U(r) = a/r¹²− b/r⁶,

где a, b − некоторые положительные константы. Сила взаимодействия двух атомов связана с потенциальной энергией соотношением F = −U_r^/, где U_r^/ − производная энергии по r. При расчете всех характеристик можно учитывать взаимодействие атома только с его ближайшими соседями.
Выразите через параметры a, b, m следующие характеристики кристалла:

1. Плотность ρ.

2. Удельную теплоту сублимации (перехода из кристаллического в газообразное состояние) λ.

3. Модуль Юнга кристалла E.

4. Максимальное относительное удлинение кристалла до его разрушения ε_пр.

5. Предел прочности на разрыв (максимальное механическое напряжение, который может выдержать кристалл без разрушения) − σ_пр.

6. Линейный коэффициент термического расширения кристалла α.

Рекомендуем использовать приближенную формулу, справедливую при малых величинах x:

(1 + x)^α≈ 1 + αx + α(α − 1)x²/2,

в которой вы можете использовать столько членов, сколько требуется в конкретной ситуации.

 

 

На рисунке изображены две изотермы вещества, совершающего фазовый переход газ-жидкость, соответствующие двум очень близким температурам T и T + ΔT. Рассмотрите цикл Карно между горизонтальными участками изотерм.

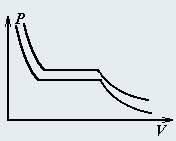
1. Покажите, что уравнение (которое называется уравнением Клапейрона-Клаузиуса), связывающее изменение давления насыщенных паров изменением температуры имеет вид

Δ/ΔT = q/{T(V₁− V₂)};

где обозначено: λ − удельная теплота перехода, V₁ и V₂ − удельные объемы газовой и жидкой фаз, соответственно.
2. Считая изменения ΔP и ΔT бесконечно малыми, полагая q независящим от температуры, V₂< < V₁, считая пар идеальным газом, найдите зависимость давления насыщенных паров воды от температуры.
3. Представьте полученную зависимость в таких координатах, чтобы она была линейной. В таблице задана зависимость давления p насыщенных паров воды от температуры t. Используя все приведенные данные, найдите удельную теплоту парообразования воды.

 

t, °C
p, Па

4. Воспользуйтесь полученным в пункте 1 уравнением для описания фазового перехода жидкость − твердое тело. Найдите на сколько надо изменить давление, чтобы температура замерзания льда изменилась на один градус. Удельная теплота плавления льда равна 332 кДж/кг.

 

 

При постоянной температуре T зависимость давления газа P от высоты h, определяется барометрической формулой

P = P_oe^−μgh/(RT),

где μ − молярная масса газа, g − ускорение свободного падения, R − газовая постоянная. Молярную массу воздуха принять равной μ = 0,029 кг/моль.
1. Оцените высоту, на которой давление воздуха уменьшается на 1 %, если температура воздуха постоянна и равна t = 0 °C.
2. В очень высоком вертикальном цилиндрическом закрытом сверху сосуде с площадью основания S находится воздух, масса которого равна m. Найдите зависимость давления газа на дно сосуда от высоты сосуда и от температуры газа.
Рассмотрите два предельных случая а) μgh > > RT; б) μgh < < RT. Дайте физическое объяснение полученным результатам.
Постройте семейства графиков зависимостей давления газа на дно сосуда от температуры (для нескольких значений высоты сосуда h) и от высоты сосуда (при различных значениях температуры T).

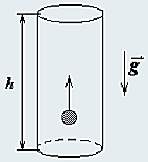
В качестве наглядной модели газа часто рассматривают множество маленьких жестких шариков, хаотически движущихся в некотором сосуде. В дальнейшем рассмотрим поведение упругого шарика движущегося вертикально в закрытом сосуде, находящемся в поле тяжести Земли. Столкновения шарика с дном и верхней крышкой сосуда будем считать абсолютно упругими. Будем изучать среднюю силу давления шарика на дно сосуда, причем будем полагать, что усреднение проводится по промежутку времени, значительно превышающему время между двумя последовательными ударами шарика.
3. Найдите зависимость силы давления шарика на дно сосуда от его высоты h и его скорости v_o у дна сосуда.
Рассмотрите предельные случаи а) mgh > mv_o²/2; б) mgh < mv_o²/2. Постройте семейства зависимостей силы давления от высоты сосуда (при постоянной v_o) и от квадрата скорости v_o² (при постоянной высоте сосуда h).
4. Рассмотрите «адиабатный» процесс уменьшения высоты сосуда с прыгающим шариком. Пусть крышка сосуда медленно опускается, найдите зависимость силы давления шарика на дно от высоты сосуда. Определите «показатель» адиабаты для этой системы. Дайте объяснение полученному результату.

 

 

1. Электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q₁ и −q₂. Покажите, что поверхность нулевого потенциала этого поля представляет собой сферу, найдите ее радиус.
2. Точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Найдите:
− суммарный индуцированный заряд сферы;
− силу взаимодействия заряда и сферы.
3. Точечный заряд q расположен на расстоянии l от центра металлической изолированной сферы радиуса R. Найдите:
− индуцированный дипольный момент сферы;
− силу взаимодействия заряда и сферы.
4. Точечный заряд q находится на расстоянии h от бесконечной плоской проводящей пластины. Найдите:
− распределение поверхностной плотности индуцированных зарядов на платине;
− силу взаимодействия заряда и пластины;
− энергию взаимодействия заряда и пластины;
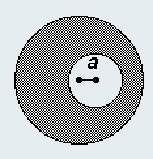
5. Внутри равномерно заряженного шара с объемной плотностью заряда ρ вырезана сферическая полость, центр которой находится на расстоянии a от центра шара. Найдите напряженность электрического поля в полости.

6. Металлический шарик радиуса r помещен в однородное электрическое поле напряженности E. Найдите:
− распределение поверхностной плотности зарядов на шарике;
− индуцированный дипольный момент шарика.
7. «Газ» состоит из одинаковых металлических шариков радиуса r, концентрация которых равна n. Среднее расстояние между шариками значительно больше их радиусов. Найдите диэлектрическую проницаемость такого «газа».
Указание. Воспользуйтесь соотношением

ε × ε_o× E = ε_o× E + P,

где P − поляризация среды (дипольный момент единицы объема).
Диэлектрическая проницаемость воздуха при нормальных условиях равна ε = 1,00058. Оцените средний размер молекул воздуха.
8. Точечный заряд q находится на расстоянии h от бесконечной плоской границы с бесконечным диэлектриком с проницаемостью ε. Найдите
− распределение поверхностной плотности поляризационных зарядов на платине;
− силу взаимодействия заряда и пластины.
9. Шар радиуса r, изготовленный из диэлектрика с проницаемостью ε, помещен в однородное электрическое поле напряженности E. Найдите:
− распределение поверхностной плотности зарядов на шарике;
− индуцированный дипольный момент шарика.
10. Небольшой шарик радиуса r, изготовленный из диэлектрика с проницаемостью ε, находится на большом расстоянии l (l > > r) от точечного заряда q. Найдите силу, действующую на шарик со стороны заряда.

 

 

Цепочка резисторов состоит из N одинаковых звеньев и подключена с одной стороны к источнику постоянного напряжения U_o, а с другой к источнику постоянного напряжения U₁.
Для построения требуемых графиков используйте следующие значения параметров R₂= 20R₁, U_o= 2U₁.

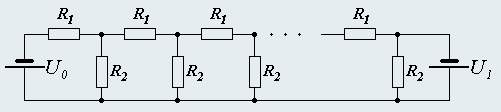
1. Найдите значения напряжений на всех резисторах R₂. Постройте схематический график зависимости напряжения от номера резистора.

2. Найдите значения напряжений на резисторах R₂, если источник U₁ отключить. Постройте схематический график зависимости напряжения от номера резистора.

3. Найдите значения напряжений на резисторах R₂, если источник U₁ заменить на резистор сопротивлением r.

4. Найдите значения напряжений на всех резисторах R₂ при N → ∞.

5. Найдите сопротивление цепи, состоящей из N звеньев. Рассмотрите случай N → ∞.

6. Допустимая погрешность расчета сопротивления цепи, состоящей из N звеньев равна ε (ε < < l). При каком числе звеньев цепочку можно считать бесконечной? Получите результат в общем виде, а затем проведите численный расчет для а) R₂= 20R₁; б) R₂= 2R₁ при предельной погрешности e = 1 %.

7. Данная задача является прекрасной моделью для описания кабеля с небольшой утечкой. При этом сопротивления R₁ описывают собственное сопротивление кабеля, а R₂ − сопротивление окружающей среды, по которой возможна некоторая утечка электрического тока.

Очень длинный медный провод диаметром a = 1 мм, покрытый слоем лака толщиной h = 20 мкм, находится в хорошо проводящей среде. Потенциал одного конца провода поддерживают равным φ_o= 100 В. Найдите зависимость силы тока в проводе от расстояния до источника x. Чему равна сила тока, потребляемая от источника? На каком расстоянии сила тока уменьшится в два раза?
Удельное электрическое сопротивление меди принять равным ρ₁= 2 × 10⁻⁸Ом•м, удельное электрическое сопротивление покрывающего лака ρ₂= 2 × 10⁸Ом•м.

 

 

Вертикальная катушка содержит N витков, высота катушки H, ее радиус a. На оси катушки находится тонкий деревянный стержень толщиной b, b < < a, по которому может скользить без трения проводящее кольцо, радиус которого чуть превышает радиус стержня. Электрическое сопротивление кольца R, индуктивность L, масса m. Если по катушке протекает переменный электрический ток круговой частоты ω с амплитудным значением силы тока I_o, то кольцо приподнимается над катушкой.
В пунктах (1) − (4) считать, что по катушке протекает постоянный электрический ток силой I.

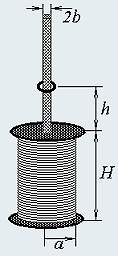
1. Найдите величину индукции магнитного поля, создаваемого одним витком катушки, на оси витка в зависимости от расстояния до центра витка.
2. Найдите зависимость индукции магнитного поля B на оси катушки от расстояния до нее h. При вычислениях воспользуйтесь формулой

∫{dx/(a²+ x²)^3/2} = x/{a²√(a²+ x²)}.

3. Считая, что h << a << H, представьте полученное выражение для индукции поля в приближенном виде B = B_o(1 + βh).
Найдите значения постоянных B_o и β.
В дальнейших пунктах используйте это приближенное выражение.
4. Найдите горизонтальную составляющую индукции магнитного поля на малом расстоянии b от оси катушки на высоте h.
Далее будем считать, что по катушке протекает переменный электрический ток круговой частоты ω с амплитудным значением силы тока I_o.
5. Пусть кольцо находится на высоте h. Найдите значение силы тока в кольце и сдвиг фаз между током в кольце и током в катушке.
6. Найдите среднюю силу, действующую на кольцо, со стороны магнитного поля.
7. Считая высоту подъема кольца малой по сравнению с высотой катушки, покажите, что зависимость высоты подъема кольца от силы тока в катушке имеет вид h = A − B/I_o². Запишите выражения для параметров A, B.

· Следующая задача

1. На двух проводящих горизонтальных параллельных рельсах, находящихся на расстоянии l друг от друга, перпендикулярно рельсам расположена проводящая перемычка массы m, которая может скользить по рельсам без трения. Вся система помещена в однородное вертикальное магнитное поле индукции B. Рельсы соединили с помощью резистора сопротивлением R, а к перемычке приложили постоянную горизонтально направленную силу F. Пренебрегая сопротивлением перемычки и рельсов и индуктивностью контура, найдите скорость установившегося движения перемычки.

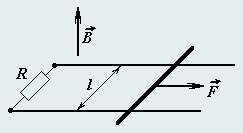
2. В системе, описанной в п. 1, резистор заменили на конденсатор емкости C. Как будет двигаться перемычка в этом случае?

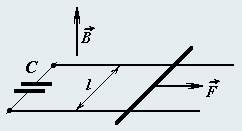
3. Замените в рассматриваемой системе конденсатор на катушку индуктивностью L и определите характер движения перемычки в этом случае.

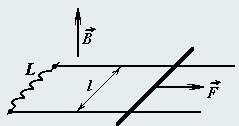
4. В установке, описанной в п. 1, перемычка покоится на некотором расстоянии x_o от резистора. Внешняя сила не действует, первоначально магнитного поля нет, а затем достаточно быстро включают вертикальное однородное магнитное поле индукции B. Как изменится расстояние между перемычкой и резистором по прошествии большого промежутка времени.

· Следующая задача

В различных приборах для фокусировки заряженных частиц используется магнитное поле. В данной задаче изучаются условия фокусировки частиц.
1. Частица массы m влетает в магнитное поле индукции B со скоростью v, направленной под углом γ к вектору индукции поля. Покажите, что траектория частицы является цилиндрической спиралью, определите ее радиус R и шаг h.
2. Пучок частиц массы m вылетает из узкой щели, расположенной в плоскости XY. Скорости всех частиц равны v и направлены в пределах плоского малого угла 2α_o, биссектриса которого перпендикулярна плоскости XY. Над плоскостью создано однородное магнитное поле индукции B, направленное параллельно пластине. Считая, что вектора скоростей всех частиц направлены перпендикулярно вектору индукции поля, покажите, что частицы будут фокусироваться на пластине. Определите положение и ширину полосы, в пределах которой частицы будут попадать на пластину.

3. Определите форму и размеры области попадания частиц на пластину в условиях, описанных в п. 2, если вектора скоростей частиц направлены внутри конуса с углом полураствора α_o.
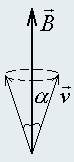
4. Пучок частиц массы m, влетает из одной точки в однородное магнитное поле индукции B, направленное вдоль оси Z. Скорости частиц равны v, а вектора скоростей частиц направлены внутри конуса с углом полураствора α_o, ось которого совпадает с направлением вектора индукции поля. Найдите ширину пучка как функцию координаты z. Считая угол α_o малым, найдите на каком расстоянии от источника частицы сфокусируются. Оцените ширину пучка в области фокуса.

Опишите прохождение световых лучей через центрированную оптическую систему состоящую из сферических преломляющих поверхностей, центры которых лежат на одной прямой, которая называется оптической осью системы. Заметим, что таким системам относятся телескопы, микроскопы, фотоаппараты, диапроекторы, глаза человека и т.д. Такие системы обладают осевой симметрией, поэтому достаточно рассмотреть ход лучей в одной плоскости, содержащей оптическую ось.
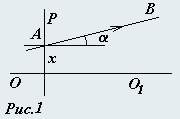
Пусть (см. рис. 1) OO₁ – оптическая ось системы, проведем произвольную плоскость P, перпендикулярную оси. Произвольный луч AB, пересекающий плоскость P однозначно определяется двумя параметрами: x – расстоянием от оптической оси до точки пересечения луча и плоскости, α – углом между направлением луча и оптической осью (договоримся отсчитывать этот угол в направлении «против хода часовой стрелки»). Очевидно, что параметры луча (x, α) могут быть как положительными так и отрицательными. Кроме того, будем полагать их малыми настолько, что везде, где это необходимо, будем считать синус и тангенс угла α равным величине самого угла, естественно, измеренному в радианах. Такое приближение называется параксиальным (близким к оси). В данном приближении в любой центрированной системе связь между параметрами одного и того же луча в разных плоскостях линейна, сколько бы преломляющих поверхностей не находилось между ними. Рассмотрите изменение этих параметров, когда луч проходит через следующие простые элементы оптической системы.

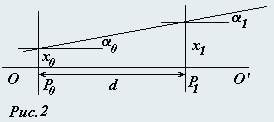
1. Участок пустого пространства. Пусть между двумя плоскостями P_o (входной) и P₁ (выходной), находящихся на расстоянии d друг от друга, преломляющих поверхностей нет (рис. 2). Установите связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча.

2 Сферическая преломляющая поверхность. Луч преломляется на сферической поверхности радиуса R, за которой находится среда с относительным (второй среды относительно первой) показателем преломления n. Установите связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча.
3. Тонкая линза. Линза представляет собой две сферические поверхности, она считается «тонкой», если можно пренебречь горизонтальным смещением луча в самой линзе, иными словами, если ее толщина значительно меньше радиусов кривизны ее поверхностей. Покажите, что связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча, прошедшего через тонкую линзу, с радиусами кривизны поверхностей R₁, R₂ и показателем преломления n, выражается формулами