Повторные испытания. Формула Бернулли

Рассмотрим случай многократного повторения одного и того же испытания или случайного эксперимента. Результат каждого испытания будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. В качестве результатов или элементарных исходов каждого отдельного испытания будем различать лишь две возможности:

1) появление некоторого события А;

2) появление события , (события, являющегося дополнением А)

Пусть вероятность P(A) появления события А постоянна и равна p (0.p1). Вероятность P() события обозначим через q: P() = 1– p=q.

Примерами таких испытаний могут быть:

1) подбрасывание монеты: А – выпадение герба; – выпадение цифры.

P(A) = P() = 0,5.

2) бросание игральной кости: А – выпадение количества очков, равного пяти, выпадение любого количества очков кроме пяти.

P(A) =1/6, P() =5/6.

3) извлечение наудачу из урны, содержащей 7 белых и 3 черных шара, одного шара (с возвращением): А – извлечение белого шара, – извлечение черного шара

P(A) = 0,7; P() = 0,3

Пусть произведено n испытаний, которые мы будем рассматривать как один сложный случайный эксперимент. Составим таблицу из n клеток, расположенных в ряд, пронумеруем клетки, и результат каждого испытания будем отмечать так: если в i-м испытании событие А произошло, то в i-ю клетку ставим цифру 1, если событие А не произошло (произошло событие ), в i-ю клетку ставим 0.

Если, например, проведено 5 испытаний, и событие А произошло лишь во 2-м и 5-м испытаниях, то результат можно записать такой последовательностью нулей и единиц: 0; 1; 0; 0; 1.

Каждому возможному результату n испытаний будет соответствовать последовательность n цифр 1 или 0, чередующихся в том порядке, в котором появляются события A и в n испытаниях, например:

1; 1; 0; 1; 0; 1; 0; 0;... 0; 1; 1; 0

n цифр

Всего таких последовательностей можно составить 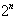(это читатель может доказать сам).

Так как испытания независимы, то вероятность P каждого такого результата определяется путем перемножения вероятностей событий A и в соответствующих испытаниях. Так, например, для написанного выше результата найдем

P = p×p×q×p×q×p×q×q×...×q×p×p×q

Если в написанной нами последовательности единица встречается х раз (это значит, что нуль встречается n–x раз), то вероятность соответствующего результата будет pnqn-x независимо от того, в каком порядке чередуются эти x единиц и n–x нулей.

Все события, заключающиеся в том, что в n испытаниях событие A произошло x раз, а событие произошло n-x раз, являются несовместными. Поэтому для вычисления вероятности объединения этих событий (или суммы этих событий), нужно сложить вероятности всех этих событий, каждая из которых равна pnqn-x . Всего таких событий можно насчитать столько, сколько можно образовать различных последовательностей длины n, содержащих x цифр "1" и n–x цифр "0". Таких последовательностей получается столько, сколькими способами можно разместить x цифр "1" (или n–x цифр "0") на n местах, то есть число этих последовательностей равно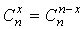

Отсюда получается формула Бернулли:

Pn(x) =

По формуле Бернулли рассчитывается вероятность появления события A "x" раз в n повторных независимых испытаниях, где p – вероятность появления события A в одном испытании, q - вероятность появления события 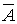в одном испытании.