Показательное (экспоненциальное) распределение

Показательным (экспоненциальным) распределением называют распределение вероятностей непрерывной св X, которое описывается плотностью вероятностей: f(x) =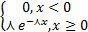

где 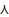> 0 - постоянная и называется параметром показательного распределения. График плотности распределения

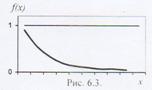
Примером непрерывной св, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где 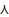- интенсивность потока. Таким образом, показательный закон лежит в основе математической модели систем массового обслуживания.

Функция распределения F(x) св, распределенной по показательному закону, равна:

F(x)=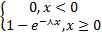

График функции распределения

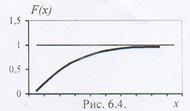
Математическое ожидание случайной величины, распределенной по показательному закону, равно М(Х)= 1/ 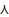,. Медиана Me=ln2/ 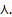Дисперсия D (X)= 1/ 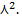Среднее квадратаческое отклонение совпадает с математическим ожиданием. Начальные теоретические моменты можно найти по ф-ле 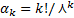. Коэффициент асимметрии равен А(Х)=2, эксцесс - Е(Х)=6.

Вероятность попадания случайной величины, распределенной по показательному закону, в интервал (α,β) определяется по формуле: P(α<X<β)=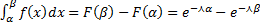

Показательный закон применяется в качестве одной из возможных математических моделей в теории надежности. Параметр 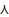в теории надежности называется интенсивностью отказа элемента.