Нормальное распределение. Нормальный закон распределения получен в связи с разработкой теории ошибок наблюдения

Нормальный закон распределения получен в связи с разработкой теории ошибок наблюдения. Случайные ошибки складываются из множества различных неконтролируемых причин: температурных колебаний, вибраций в окружающей среде, неточности измерительной шкалы прибора и т. д. Если каждая из этих случайных причин оказывает на результаты измерений незначительное влияние по сравнению с общим эффектом, то их сумма (случайная ошибка) подчинена закону, близкому к нормальному (для появления нормального распределения необходимо выполнение дополнительных условий).

Непрерывная случайная величина имеет нормальное распределение вероятностей с параметрами а и >0. если её плотность распределения вероятностей имеет вид:

 

(6.7)

Кривая распределения - это кривая Гаусса, которая имеет симметричный колоколообразный вид.

Из формулы (6,7) следует, что кривая f(x) достигает максимум в точке (α,1/ ) имеет две точки перегиба (α± 1/()) Плотность распределения f(х) симметрична относительно прямой х = а, те f(а+у) f(а-у). Если х -> ± 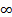, то f(х)-> 0.

С ростом f(х) уменьшается, а т. к. площадь, ограниченная всей кривой и осью Ох. равна 1. то с увеличением кривая «растягивается» вдоль оси Ох. При уменьшении кривая вытягивается вверх вдоль прямой х= а, но «сжимается» в горизонтальном направлении. Если зафиксировать а изменять а, то кривая будет смешаться в горизонтальном направлении, сохраняя форму. Следовательно, параметр характеризуег форму кривой, а а - ее положение.

Функция распределения F(х) нормально распределенной случайной величины X имеет вид:

Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:

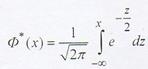
называемую нормированной функцией нормального распределения с параметрами а=0 и =1 или через функцию Лапласа:

Функция распределения св Х, подчин нормальному закону с параметрами а и , можно выразить через Ф^* (x):

Как и всякая функция распределения, функция Ф^* (x) неубывающая, непрерывная слева удовлетворяет условиям Ф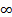^* (- )=0, Ф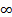^* () = 1, кроме того, Ф^* (-х)=1- Ф^* (х).

График значения функции Лапласа

Математическое ожидание, мода и медиана нормально распределенной св равны М(Х)= Мо = Ме= а. Дисперсия D(X) = , стандартное отклонение 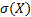= . Коэффициент асимметрии и эксцесс равны нулю.

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный интервал (α,β) определяется с помощью нормированной функции нормального распределения по формуле:

или через функцию Лапласа:

(интегральная теорема Лапласа)

Где ,

Вероятность того, что отклонение нормально распределенной св X поабсолютной величине меньше заданного положительного числа равна:

или

Из полученных формул следует, что чем меньше , тем больше вероятность принять значение принадлежащее интервалу (а — , а + ).

Правило 3-х (трех"сигм"). Пусть имеется нормально распределённая случайная величина X с

математическим ожиданием, равным а и дисперсией . Определим вероятность того, что X принимает

значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических

отклонения.

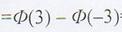
Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на З .

(Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8. 2.9 или 3.2 и получить тот же вероятностный результат. Учитывая, что Ф(2)=0,477. можно было бы говорить и о правиле 2-х "сигм".).

Нормальное распределение играет большую роль в теории вероятностей и ее применениях. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет «примерно» нормальное распределение.

 

23. Распределение х²

Пусть имеется nнезависимых случайных величин Х1,Х2,...,Xn, распределенных по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Тогда случайная

величина x² = распределена по закону, который называется "распределение х²" («хи-квадрат»)

или «распределение Пирсона». Очевидно, что она может принимать лишь неотрицательные знач.

Число v =п называется числом степеней свободы.

Плотность вероятностей случайной переменной, имеющей распределение x² и v степеней свободы.

выражается формулой:

 

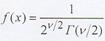
где Г(а)- гамма-функция.

Таким образом, распределение х,² зависит только от одного параметра - числа степеней свободы v. И чем больше v, тем более симметрично распределение x², хотя некоторая правая асимметрия присутствует всегда. При п > 1 график плотности распределения случайной величины x² представляет собой кривую, изображенную на рисунке

Математическое ожидание распределения х² равно М(Х) = v , дисперсия D(Х) = 2v, асимметрия и эксцесс соответственно равны: А(Х) = , Е(Х) = 12/v.

Отмстим, что если n —> 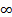, то распределение отношения стремится к нормированному нормальному закону распределения.

Для того чтобы определить вероятность попадания случайной величины x² в какой-либо промежуток из множества положительных чисел, пользуются таблицей распределения x².