Теоремы Хинчина, Маркова, Колмогорова

Теорема Хинчина. Пусть Х1,Х2,….,Х_n,... - независимые, одинаково распределенные св, имеющие конечные математические ожидания М(Хi)=m. Тогда последовательность {Y_n}, где

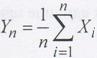сходится к т с вероятностью 1, т.е. для любого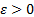

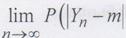
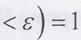
Закон больших чисел может быть распространен и на независимые случайные величины.

Теорема Маркова. Если для случайных величин Х1,Х2,…,Х_n,...

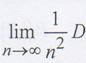
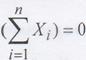
то среднее арифметическое наблюденных значений случайных величин сходится по вероятности среднему арифметическому их математических ожиданий, т.е. для любого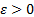

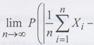
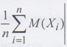
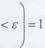
Большое значение в теории вероятностей играют сформулированные Колмогоровым достаточные условия для существования усиленного закона больших чисел: последовательность случайных величин Х1,Х2,….,Х_n,... подчиняется усиленному закону больших чисел, если с вероятностью 1 при n —>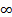

Теорема Колмогорова. Если последовательность взаимно независимых величин Х1,Х2,….,Х_n,...

удовлетворяет условию

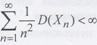то она подчиняется усиленному закону больших чисел.

Из теоремы Колмогорова следует утверждение: существование математического ожидания является необходимым и достаточным условием для применимости усиленного закона больших чисел к последовательности одинаково распределенных и взаимно независимых случайных величин.

Усиленный закон больших чисел имеет большое принципиальное значение, т.к., согласно этому закону, существует лишь конечное число случаев, когда среднее арифметическое случайных величин будет отличаться от среднего арифметического математических ожиданий.