Прямо пропорційна функція, її графік і властивості

Лінійну функцію, що задається формулою 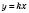, де , називають прямою пропорційністю.
Графік прямої пропорційності — пряма, що проходить через початок координат. Якщо , графік лежить у I і III координатних чвертях, а якщо 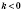— то у II і IV координатних чвертях.
Приклади
1) , , .
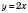2) , , .

Обернено пропорційна функція, її графік і властивості.

Функцію, задану формулою , де х — незалежна змінна, — дане число, називають оберненою пропорційністю.
Область визначення функції — множина всіх чисел, крім 0.
Графік функції — гіпербола, симетрична відносно початку координат. Коли , вітки такої гіперболи розміщені в I і III координатних кутах, коли 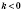— у II і IV.
Як приклад побудуємо графік функції . Заповнимо таблицю (значення x задаємо, y — обчислюємо за формулою :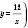

x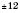
y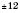

Нанесемо отримані точки на координатну площину. Сполучивши ці точки плавною лінією, отримаємо графік (див. рисунок):

Зверніть увагу на поводження графіка поблизу осей координат. Графік до них нескінченно наближається, але не перетинає. Дійсно, не входить до області визначення, отже точки перетину з віссю Oy немає. 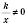ні при якому значенні х, значить, якщо , точки перетину з віссю Ox немає.