Экспоненциальное распределение

Наибольшее распространение получило экспоненциальное (показательное) распределение, при котором функция распре­деления наработки до отказа имеет вид

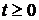, (3.1)

где – параметр этого распределения, характеризующий число отказов объекта в единицу времени.

Согласно (2.5) соответствующая плотность распределения

. (3.2)

Согласно (2.3) функция надежности

. (3.3)

Согласно (2.7) и (2.9) вероятность отказа объекта до мо­мента и вероятность безотказной работы до момента соот­ветственно будут

;

Согласно (2.17) средняя наработка до отказа

, (3.4)

т. е. равна величине, обратной параметру экспоненциального распределения.

Из (2.13) следует, что интенсивность отказов

является постоянной величиной, не зависящей от времени и чис­ленно равной параметру распределения и, как видно из (3.4), обратной средней наработке до отказа.

Графики показателей надежности при экспонен­циальном распределении даны на рис. 3.1.

Данным распределением описываются объекты, где можно не учитывать ни период приработки, ни участок старения и износа (например, управляющие контроллеры). Экспоненциальное распределение хорошо описывает время безотказной работы сложных систем, состоящих из большого числа разнородных компонентов. Одна из причин широкого применения этого распределения его простота.