2018-01-21
554
Силу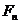 
переносим по линии действия на ось симметрии зуба и раскладываем на составляющие 
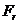и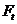 
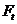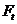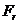. При этом радиус приложения окружной силы будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил и . Напряжение в опасном сечении, расположенном вблизи хорды основной окружности:
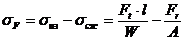
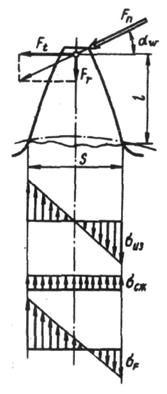
где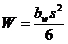 
‑ момент сопротивления сечения при изгибе;
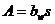‑ площадь.
Знак «-» в формуле указывает, что за расчетные напряжения принимают напряжения на растянутой стороне зуба, так как в большинстве случаев практики именно здесь возникают трещины усталостного разрушения (для стали растяжение опаснее сжатия).
Размеры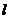 
и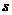 
неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, их выражают через безразмерные коэффициенты:
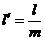и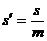 
где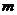 
‑ модуль зубьев.
После подстановки и введения расчетных коэффициентов получают
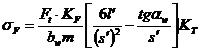
где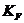 
‑ коэффициент расчетной нагрузки;
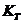‑ теоретический коэффициент концентрации напряжений.
Далее обозначают
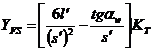‑ коэффициент формы зуба (для наружных зубьев рис. 8.20).
Для колес с внутренними зубьями приближенно можно принимать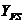 
= 3,5…4большие величины ‑ при меньших z.
При этом для прямозубых передач расчетную формулу записывают в виде
(**)
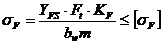где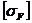 
‑ допускаемое напряжение изгиба (см. § 8.13).
Особенности расчета косозубых передач
