2018-01-21
541
Структуризация систем управления представляет собой выделение независимых подсистем, которые функционируют самостоятельно на различных режимах. В этом случае систему можно рассматривать как многоконтурную с вложенными контурами. Каждый внутренний контур имеет быстродействие на порядок больше внешнего контура. В этом случае время переходного процесса во внутреннем контуре на порядок меньше времени регулирования во внешнем контуре.
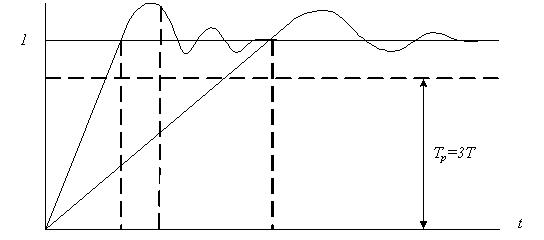
Рис. Переходные процессы в короткопериодическом внутреннем и длиннопериодическом внешнем контурах структуризованной системы
На современных самолетах используются режимы автоматического, полуавтоматического и ручного управления.
Рассмотрим электрический привод, описываемый уравнением:
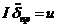, где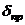 
– угол поворота вала привода.
Закон управления приводом:
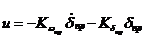
Собственное возмущенное движение привода с гибкой обратной связью описывается уравнением:
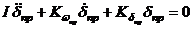
В этом случае привод с гибкой обратной связью обладает собственной частотой и коэффициентом относительного демпфирования:
; 
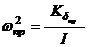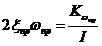
Обычно выбирают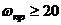 
; 
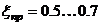
Для управления короткопериодическим угловым движением самолета используется соотношение между желаемой частотой привода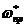 
и частотой короткопериодического углового движения самолета с автоматикой 
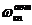в соответствии с неравенством:
; 
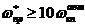
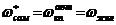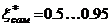(2 контур)
Для траекторного контура желаемая частота длиннопериодического колебательного движения выбирается на один – два порядка меньше частоты короткопериодического углового движения самолета
; 
; 
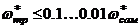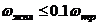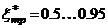(3 контур)
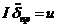
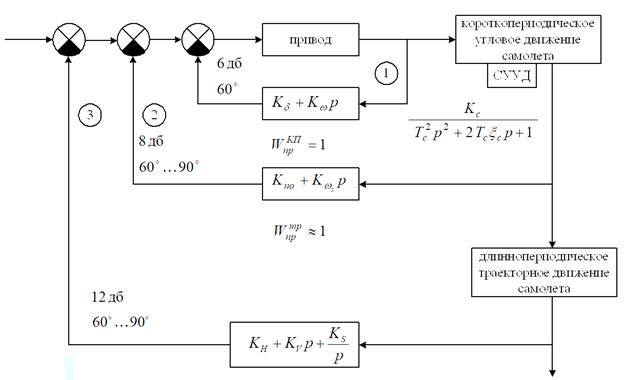
Рис. Схема системы управления самолета с вложенными контурами управления следящим электрическим приводом, системой улучшения устойчивости и управляемости углового движения и астатической системы стабилизации высоты
При синтезе траекторного контура передаточной функции привода и самолета в угловом движении считаются идеальными. Выполняется расчет управляющего устройства (контролера), который включает в закон управления позиционный сигнал по высоте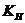 
, коэффициент усиления 
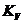по скорости набора высоты vy и изодромный интегральный сигнал от ошибки регулирования высоты с коэффициентом усиления 
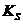, позволяющий создать астатизм и обеспечить нулевую среднюю ошибку стабилизации.
2.5 Исследование устойчивости для систем порядка n
Рассматривается линейная стационарная система, движение которой описывается системой n дифференциальных уравнений в форме Коши, разрешенных относительно производных
= 
Элементы матрицы динамических коэффициентов А не зависят от времени:
A =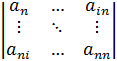 
С использованием программы damp вычисляем собственные значения матрицы динамических коэффициентов А
damp (A)
Собственные значения матрицы динамических коэффициентов А могут быть вещественного либо комплексного типа
= 
= 
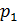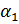
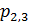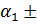j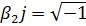 
2.5.1 Корневой анализ системы порядка n
Динамическая система имеет n- корней, из которых k – число вещественных корней и n- k – число комплексно сопряженных корней. Если все корни имеют вещественную отрицательную часть, то динамическая система устойчива. Если хотя бы один корень положительный, то система неустойчива.
x =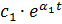 
+ 
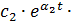sin( 
)
число колебательных форм движения
L =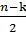 
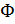= k + L
= 
, = 
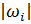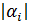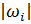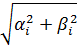
Система порядка n имеет k апериодических форм движения с частотой среза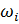 
= 
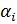, равной модулю вещественной части корня, и L = 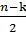колебательных форм движения с частотой среза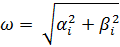 
Все формы ранжируются в порядке возрастания частоты 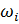от минимальной до максимальной. Главной является 1-я форма с минимальной частотой. Если этой частоте соответствует вещественный корень, то 1-я форма естьапериодическое движение, а если собственное значение – комплексно-сопряженнаявеличина, то 1-я форма представляет собой колебательное движение.
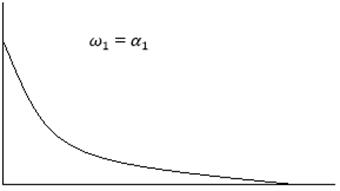
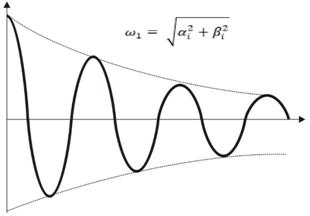
Рис. Варианты первой формы движения апериодического и колебательного типа.
Результатом частотного анализа собственных значений является:
1. Устойчивость системы, если все вещественные части корней – отрицательны.
2. Определение 1-ой формы движения по величине минимального по модулю собственного значения частоты 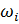(где форма движения может быть апериодической или колебательной в зависимости от того, каким является минимальный по модулю корень (вещественным или комплексно-сопряженным))
3. Определение числа апериодических форм движенияk и колебательных форм движения L
4. Для каждой формы колебательного движения определяются значения частоты и коэффициента относительного демпфирования.
5. Для систем с автоматикой требуется, чтобы коэффициент относительного демпфирования составлял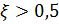 
для истребителей, 
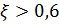для пассажирских самолетов и не превышал 
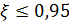для самолетов всех типов.
Пример:
Угловое движение по крену самолета с приводом элеронов.
= a 
+ b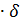 
= 
= 
= - 
– 
+ 
, 
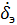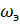
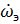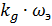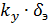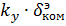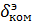– командный сигнал
+ 
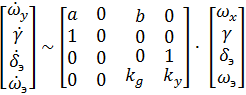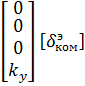
A =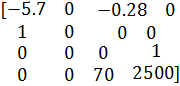 
damp (A)
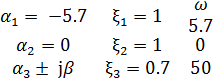
После линейного анализа на устойчивость разомкнутой системы решается задача синтеза системы управления по заданным техническим характеристикам и критериям устойчивости.
