2018-01-21
460
Математическая модель в пространстве состояний представляет собой дифференциальное уравнение в матричной форме:
U
0 1 0 0 0 0 
0
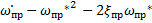0 0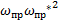 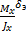0 0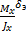 
= 
0 0 0 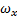0 = 
+ 0 
0 0 1 0 0 0 
0
0 0 0 
0 0 
0
0 0 0 0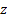 
0 
0
А В
В системе MatLab необходимо ввести значение элементов матрицы или использовать арифметические операции над известными числами.
Ввод данных: b
U
a = [0 1 0 0 0 0 [0
-32* 
-2*0,7*32 0 0 0 0 32*
-0,32 0 -0,65 0 0 0 * 0
0 0 1 0 0 0 0
0 0 0 0,8 /200 0 0 0
0 0 0 0 -200 0] 0]
Где a – матрица динамических коэффициентам, b – матрица коэффициентов управления.
Требования к желаемым частотам и коэффициентов демпфирования удобно описывать в виде передаточной функции.
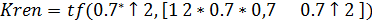
Данные передаточной функции описывают желаемые траекторные движенияпо изолированным формам движения привода, движения крена и относительно линии пути.
Суммарное движение: 
Расчет полюсов и собственных значений: 
Определение требуемых коэффициентов усиления: 
Анализ характеристик замкнутой системы управления
Модель пространства состояний:
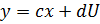, где 
– матрица измерений, 
– матрица влияния управления.
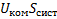x
-
Рис. Схема системы управления
Определяем матрицу динамических коэффициентов замкнутой системы:
ltivies(step,impulse,bode)
MatLab позволяет скопировать разработанную программу в документ Word и туда же вставить полученные рисунки, опции и копируемые фигуры для отчета о синтезе и анализе результата.
