

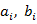 , -коефіцієнти (параметри моделі, 0 ≤ m<n,, n -порядок моделі,
, -коефіцієнти (параметри моделі, 0 ≤ m<n,, n -порядок моделі, 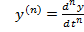 , (2.1)
, (2.1)
- лінійне неоднорідне диференційне рівняння n- го порядку.
Права частина цього рівняння визначає зовнішню дію на систему.
Cтаціонарні системи - значення параметрів незмінні:
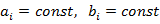 ,
, 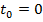 .
.
Нестаціонарні системи - параметри є функціями часу,
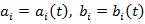 .
.
У разі, коли 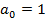 ,, рівняння (2.1) називається приведеним.
,, рівняння (2.1) називається приведеним.
Для спрощення застосовують операторну форму.
Оператор диференціювання, 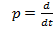 ,
, 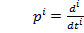 .
.
Рівняння ВВ (2.1) в операторній формі:
 (2.2)
(2.2)
= 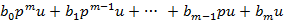 .
.
Або 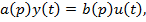 (2.3)
(2.3)
де a 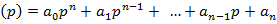 , (2.4)
, (2.4)
b 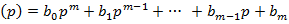 . (2.5)
. (2.5)
Загальне рішення лінійного неоднорідного диференційного рівняння n- го порядку з постійними коефіцієнтами є сумою загального рішення відповідного однорідного рівняння і частинного рішення неоднорідного рівняння:
Відповідне однорідне рівняння:
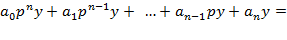 0.
0.
Однорідне рівняння описує динаміку системи при умові, що зовнішня дія на неї відсутня. Для його вирішення використовують підстановку Ейлера, а саме:
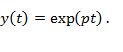 Ця підстановка приводить розв’язання лінійного диференційного рівняння до алгебраїчного рівняння
Ця підстановка приводить розв’язання лінійного диференційного рівняння до алгебраїчного рівняння
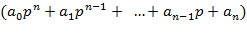 exp(pt)=0.
exp(pt)=0.
Або 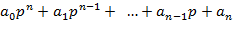 = 0. (2.6)
= 0. (2.6)
У виразі 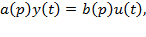 а(p) і b(p) мають спеціальні назви.
а(p) і b(p) мають спеціальні назви.
а(р) - характеристичний поліном диференціального рівняння (2.1) або власний оператор
a  .
.
Корені рівняння (2.6) а(р)=0 називають полюсами системи (2.1).
У загальному випадку рівняння а(р)=0 маємає n комплексних коренів 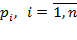 .
.
b(p) -характеристичний поліном правої частини (2.1)
або оператор дії:
b 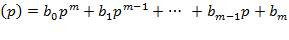 .
.
Корені рівняння b(р)=0 називають нулями системи (2.1).
У загальному випадку рівняння b(р)=0 має m комплексних коренів 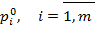 .
.
Передавальна функція
З виразу (2.3) 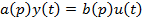 знайдемо явний зв’язок вихідної та вхідної змінної:
знайдемо явний зв’язок вихідної та вхідної змінної:

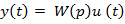 .
.
або  =
= 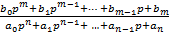 (2.8)
(2.8)
передавальна функція в операторній формі.
З (2.7) випливає 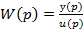 .
.
У лекції 5 передавальна функція буде розглянута детальніше.
 2018-01-21
2018-01-21 753
753








