Диференціальні рівняння (8.3) називають рівняннями стану, (8.4) називають рівнянням виходу. (8.3), (8.4) – найпростіша модель стан –вихід

• У більш загальному випадку модель стан-вихід має вигляд:

,

,

,

…

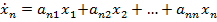, (8.5)

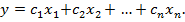(8.6)

• Вектор 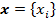= 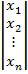називається вектором стану.

• Вектор x є елементом n -вимірного (векторного) простору , який називають простором стану.

• У цьому просторі кожній точці відповідає набір значень (координати точки) або вектор x(t).

• Стан системи в момент часу t можна позначити точкою у просторі станів. При зміні стану системи з часом точка буде рухатись у просторі.

Рівняння (8.5), (8.6) можна представити у більш компактному векторному вигляді:

(8.7)

(8.8)

де матриця системи А має розмір :

,

- матриця розміру

Для стаціонарних систем рішення рівнянь (8.7), (8.8) має вигляд:

(8.9)

. (8.10)

Формули (8.9) - (8.10) визначають перехідні процеси системи. Графічно вони можуть бути представлені у вигляді:

• часових діаграм (рис. а);

• фазових траєкторій (інтегральних кривих) (рис.б).

• Фазовою траєкторією, або інтегральною кривою в , називається лінія, яку описує вектор стану x в просторі станів при зміні часу Тобто це- годограф вектор - функції по параметру t.

• Фазовий портрет - це сукупність фазових траєкторій, що відповідають різним початковим умовам .