Поняття простору станів і моделі стан-вихід

Розглянемо автономну динамічну систему з виходом y(t):

ОК

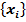y(t)

+....+ y =0 (8.1)

• Змінними стану автономної динамічної системи з виходом у називаються незалежні змінні такі, що значення вихідної змінної y(t) в довільний момент часу однозначно визначається числами = .

Стан системи в момент часу характеризується повним набором змінних стану , а початковий стан – числами .

• За визначенням, знаючи початковий стан системи, можна єдиним чином відшукати значення вихідної змінної y в будь-який момент часу : .

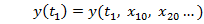• Oсобливістю змінних стану є те, що для передбачення поведінки системи в будь-який момент часу (і управління системою) достатньо інформації про змінні стану в момент і не потрібне знання передісторії процесів.

• Загальне число змінних дорівнює порядку диференціального рівняння (8.1). Лінійні комбінації і інші функції від змінних , що доповнюються до вже обраного набору, не є змінними стану, так як не відповідають умові незалежності.

• В якості змінних стану автономної системи можуть бути вибрані, зокрема, фазові змінні, тобто вихідна змінна системи y(t) і її похідні:

.(8.2)