Аперіодична (інерційна) динамічна ланка

• Аперіодична ланка першого порядку (інерційна ланка) -ланка, яка описується диференційним рівнянням:
Передавальна функція ланки: К – коефіцієнт підсилення, T – постійна часу.
Часові характеристики:
перехідна h k t	імпульсна ω   k/T
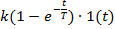
h(t)=	(t)=

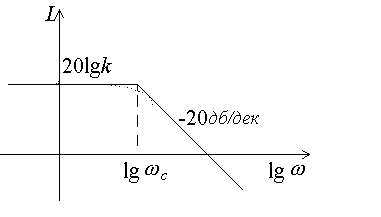
Частотні функції аперіодичної ланки 1 порядку

• • • • •

• Приклади аперіодичних ланок І –го порядку (інерційних ланок): а) RC – ланцюжок, б) LR - ланцюжок, в) двигун без врахування індуктивного опору якоря, г) резервуар компресора

Диференційна динамічна ланка

• Диференційна ланка -ланка, вихідна величина якої дорівнює швидкості зміни вхідної величини. Вона описується диференційним рівнянням:

• Передавальна функція ланки:

• Часові функції:

• Частотні функції:

Реалізувати ідеальну диференційну ланку практично неможливо, оскільки будь-яка

реальна система має кінцевий проміжок дії.

• Реальна диференційна ланка описується рівнянням

• Передатна функція ланки

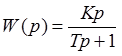
К – коефіцієнт підсилення,

T – постійна часу.

• Прикладами диференційних ланок є заслінка в потоці рідини чи газу, кут відхилення якої пропорційний швидкості руху, трансформатор напруги. Реальні диференційні ланки: а) CR ланцюжок, б) RL ланцюжок, в) трансформатор, г) заслінка в потоці рідини чи газу, д) диференційний підсилювач.