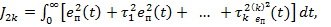 (14.2)
(14.2)
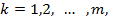
де 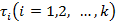 - вагові константи.
- вагові константи.
Після обчислення інтеграла за допомогою формули Парсеваля отримаємо деяку функцію від параметрів
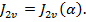
Тут α означає вектор, компонентами якого є параметри системи.
Рівність Парсеваля. Розглянемо рівність Парсеваля. яка використовується при обчисленні інтегральних квадратичних оцінок. Якщо 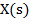 є зображенням Лапласа функції x (t) і його полюси розташовані в лівій півплощині, то справедлива рівність Парсеваля
є зображенням Лапласа функції x (t) і його полюси розташовані в лівій півплощині, то справедлива рівність Парсеваля
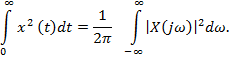
На параметри системи можуть бути накладені обмеження у вигляді рівностей і нерівностей:
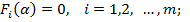
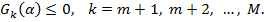
Тому в загальному випадку розглянута задача синтезу зводиться до наступної задачі на умовний мінімум:
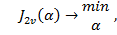
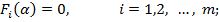
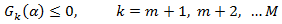 (14.3)
(14.3)
Це завдання може бути вирішене різними способами.
Замінимо нерівності (14.3) рівностями. Для цього вводяться додаткові невідомі параметри 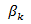 :
:
 .
.
Задача (14.3) приймає вигляд:
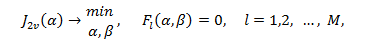 (14.4)
(14.4)
де 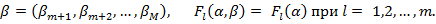
Завдання (14.4) в принципі може бути вирішене методом невизначених множників Лагранжа. Відповідно до цього методу складається функція Лагранжа
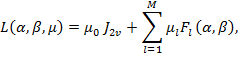
і задача (6.4) зводиться до задачі на безумовний екстремум
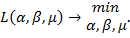
Тут 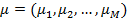 и
и 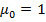 в особливому випадку (тобто коли постановка задачі має сенс).
в особливому випадку (тобто коли постановка задачі має сенс).
Приклад 14.1. За умови, що 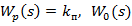 =
= 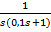 і
і 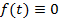 визначити параметр
визначити параметр 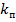 , при якому перехідний процес системи (див. рис. 5.1) є аперіодичним та інтегральна квадратична помилка
, при якому перехідний процес системи (див. рис. 5.1) є аперіодичним та інтегральна квадратична помилка 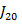 приймає мінімальне значення.
приймає мінімальне значення.
Рішення. Перехідний процес буде аперіодичним, якщо корені характеристичного рівняння розглянутої системи
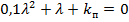
будуть речовими, тобто якщо детермінант цього рівняння 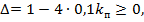 або
або 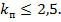
Так як 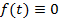 , то помилка
, то помилка 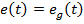 . Об'єкт включає інтегруючу ланку. Тому система є астатичной щодо задаючого впливу та статична помилка e_
. Об'єкт включає інтегруючу ланку. Тому система є астатичной щодо задаючого впливу та статична помилка e_ 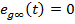 . Перехідна складова помилки
. Перехідна складова помилки
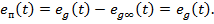 Переходячи до зображень Лапласа,отримаємо
Переходячи до зображень Лапласа,отримаємо
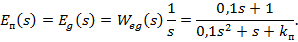
Отже, 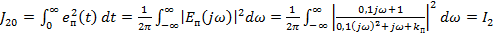
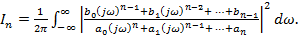 (14.5)
(14.5)
Цей інтеграл обчислюється за допомогою теорії відрахувань і для 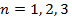 має наступний вигляд
має наступний вигляд
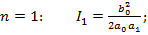 (14.5 a)
(14.5 a)
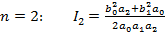 ; (14.5 б)
; (14.5 б)
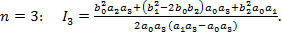 (14.5в)
(14.5в)
У даному випадку (див. (14.5)) 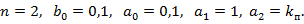
Тому (див. (4.176)) 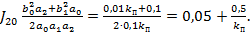
Вочевидь, що 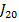 приймає мінімальне значення за умови
приймає мінімальне значення за умови 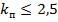 , коли
, коли 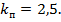
 2018-01-21
2018-01-21 477
477








