Метод синтезу систем управління максимального ступеня стійкості

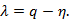Метод вирішення цього завдання заснований на перетворенні характеристичного полінома шляхом підстановки При цій підстановці перетворений поліном

(14.15)

стає маргінально стійким поліномом.

І для виписуються умови маргінальної стійкості, включаючи умови (14.8), (14.12) і (14.14):

(14.16а)

(14.16б)

(14.16в)

Тут 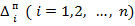- визначники Гурвіца перетвореного полінома

Коефіцієнти вихідного характеристичного полінома залежать від параметрів регулятора, а коефіцієнти перетвореного полінома залежать ще й від ступеня стійкості η.

Розглянутий метод полягає в наступному: вирішується система (14.16а) - (14.16в) щодо невідомих параметрів регулятора і ступеня стійкості η і знаходяться рішення, у яких η має найбільше значення.

При використанні цього методу важливо знати максимально можливе значення 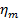, яке може прийняти ступінь стійкості.

Твердження 6. При фіксованих 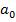і ступені стійкості η сталого полінома Q (λ) приймає максимально можливе значення, рівне

(14.17)

коли речові частини всіх нулів Q (λ) рівні між собою.

Максимально можливе значення 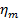будемо також називати граничним значенням

Пошук рішення задачі синтезу максимального ступеня стійкості слід починати з випадку, коли ступінь стійкості приймає граничне (максимально можливе) значення. Це можливо, коли всі нулі вихідного полінома мають однакові дійсні частини або нулі перетвореного полінома розташовуються на уявної вісі. в силу твердження 5 умову маргінальної стійкості (14.16) можна представити у вигляді

(14.18а)

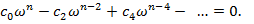(14.18б)

Якщо система (14.18а), (14.18б) не має рішення, то потрібно перейти до системи (14.16а) - (14.16в) і вирішити її при

У загальному випадку (14.16а) - (14.16в) і (14.18а), (14.18б) є необхідними, але не достатніми умовами граничної стійкості полінома 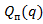. Тому, вирішивши систему (14.16а) - (14.16в) або (14.18а), (14.18б), потрібно переконається, що при знайдених значеннях параметрів серед особливих нулів полінома немає правих нулів.

При вирішенні систем (14.16а) - (14.16в) і (14.18а). (14.18б) ω розглядається як (речовий) параметр. Якщо вдається знайти необхідне рішення зазначених систем при ω ≠ 0, то це означає, що рівняння має щонайменше два дійсних кореня. І в цьому випадку зазначену додаткову перевірку потрібно проводити тільки при l ≥ 6 або n ≥ 6, коли l = n.