Внутренние силовые факторы

Обратимся теперь к случаю стержня.

Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу , равную главному вектору и пару сил с моментом , равным главному моменту системы.

Проектируя и на координатные оси, получаем в общем случае 6 алгебраических величин - 6 внутренних силовых факторов:

- нормальная сила;

и - поперечные силы;

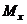и 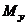- изгибающие моменты;

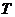- крутящий момент.

Очевидно, что, так как внутренние силы уравновешивают внешние силы, приложенные к отсеченной части, то внутренние сило-

вые факторы можно определить следующим образом:

Нормальные и поперечные силы равняются по величине сумме проекций всех внешних сил, лежащих по одну сторону от сечения, на соответствующую ось.

Изгибающие и крутящий момент определяются как суммы мо-

ментов всех сил, расположенных по одну сторону от сечения относи-

тельно соответствующих осей.

Напряжение.

Мерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.

Рассмотрим тело, находящееся под действием системы уравновешенных сил.

Будем исследовать внутренние силы в малой области, окружающей точку А. Проведем через данную точку сечение не-которой поверхностью. Внешняя нормаль этой поверхности в точке А - Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку . Результирующая внутренних сил, действующих на площадке пусть равняется .

Делим результирующую силу на , получаем величину среднего напряжения по площадке . Величина зависит от размеров площадки, перейдем к пределу, стягивая площадку к точке

Величина - называется вектором напряжения в данной точке по площадке с внешней нормалью .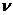

Очевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.

Совокупность всех векторов напряжения по площадкам, про-

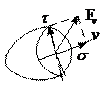ходящим через данную точку, составляет напряженное состояние в данной точке.

Величину обычно раскладывают на две составляющие: нормальное напряжение направленное по внешней нормали к площадке и касательное напряжение , лежащее в плоскости площадки.