2018-01-21
1240
Будем рассматривать случай (так называемого) нестесненного кручения, когда деформации стержня в направлении его оси не затруднены. В таком случае в поперечных сечениях стержня возникают только касательные напряжения. Этот факт можно принять за первое допущение, используемое нами в дальнейшем выводе.
Второе допущение имеет геометрический характер и состоит в том, что поперечные сечения при кручении остаются плоскими и их радиусы не искривляются.
Как показывает точное решение задачи методами теории упругости, для круглых поперечных сечений эта гипотеза выполняется абсолютно точно.
Нашей задачей будет определение напряжений и перемещений в закручиваемом стержне.
Рассмотрим произвольный стержень круглого поперечного сечения.
Выделим кольцеобразный малый элемент, а из него в свою очередь элемент m, npо который в пределе
можно считать плоским. Данный элемент содержит точку, напряженное состояние которой мы исследуем. Полярный радиус исследуемой точки 
.
Основываясь на первом принятом допущении, заключаем, что элемент mnpq испытывает чистый сдвиг.
|
|
|
Рассмотрим геометрическую сторону задачи.
При кручении поперечные сечения, между которыми заключен элемент повернутся друг относительно друга на малый угол d 
. Очевидно, что угол сдвига будет равен 
.
Величину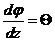 
называем относительным углом закручивания. 
Тогда 
(1).
Рассмотрим физическую сторону задачи. Будем полагать материал линейно упругим и примем закон Гука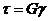 
(2).
Подставим (1) в (2): 
(3).
Мы видим, что касательные напряжения по радиусу меняются линейно, но величина Q нам еще не известна.
Обратимся к статической стороне задачи и рассмотрим равновесие отсеченной части стержня 
Интеграл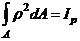 
- полярный момент инерции.
В результате получаем так называемую основную зависимость при кручении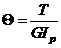 
(4)
Величина 
называется жесткостью при кручении.
Подставим (4) в (3) и получим закон распределения касатель-
ных напряжений 
(5)
Как мы выяснили ранее, закон распределения напряжений линейных и наибольшие касательные напряжения возникают на контуре сечения при 
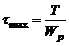(6)
Где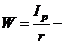 
полярный момент сопротивления.
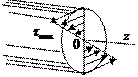Выразим 
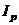и 
через диаметр
Само собой, что закон распределения касательных напряжений осесимметричный и по каждому из радиусов напряжения распределяются одинаково.
Формула (6) дает возможность рассчитывать на прочность стержни, работающие на кручение, которые называют валами.
Условия прочности при кручении выглядит: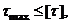 
где [ 
-допускаемое напряжение на кручение.
Может стоять задача определения коэффициента запаса по текучести. Тогда 
, где 
предел текучести при кручении.
|
|
|
